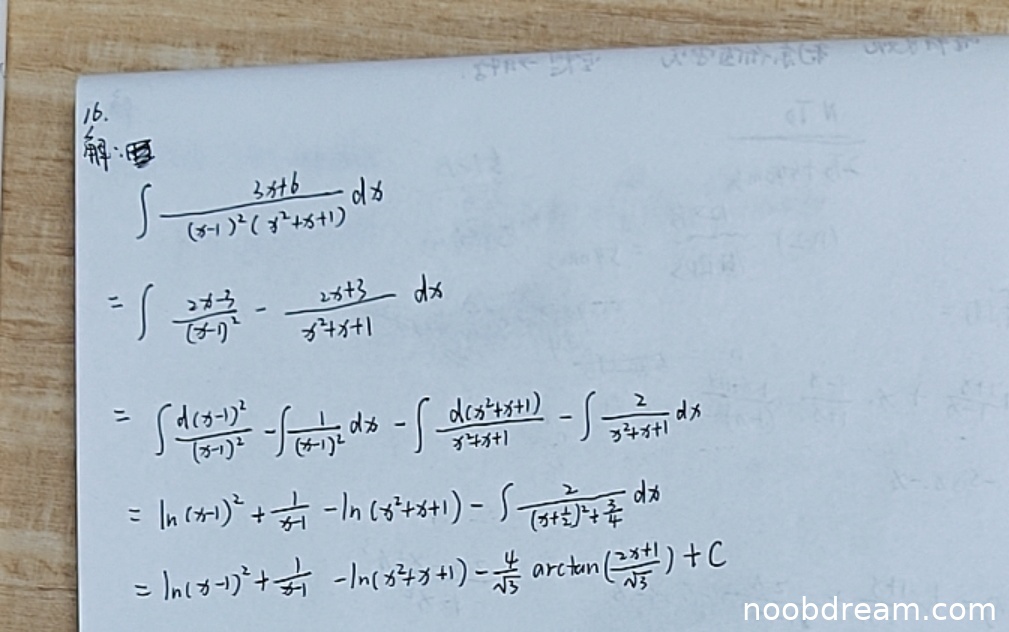
评分及理由

（1）得分及理由（满分10分）

本题旨在考察有理函数的不定积分，核心步骤是部分分式分解和逐项积分。学生的作答思路正确，即先将被积函数分解为部分分式之和，然后分别积分。然而，在具体执行过程中出现了多处关键性的逻辑和计算错误，导致最终结果与标准答案不符。

具体扣分点如下：

1. 部分分式分解错误（扣3分）：学生给出的分解形式为 \(\frac{2x-3}{(x-1)^2} - \frac{2x+3}{x^2+x+1}\)。正确的分解应设为 \(\frac{A}{x-1} + \frac{B}{(x-1)^2} + \frac{Cx+D}{x^2+x+1}\)。通过通分比较系数，可解得 \(A = -2, B = -3, C = 2, D = 3\)。因此，正确的分解应为 \(-\frac{2}{x-1} - \frac{3}{(x-1)^2} + \frac{2x+3}{x^2+x+1}\)。学生的分解从第一步就错了，这是根本性的逻辑错误。
2. 积分过程错误（扣2分）：基于错误的分解，后续的积分变形也出现错误。例如，学生将 \(\frac{2x-3}{(x-1)^2}\) 拆分为 \(\frac{d(x-1)^2}{(x-1)^2} - \frac{1}{(x-1)^2}dx\)，这是不正确的。实际上，\(\frac{d(x-1)^2}{(x-1)^2} = \frac{2(x-1)dx}{(x-1)^2} = \frac{2}{x-1}dx\)，这与原式不符。积分过程中对 \(\frac{1}{(x-1)^2}\) 的积分结果应为 \(-\frac{1}{x-1}\)，学生写成了 \(+\frac{1}{x-1}\)，符号错误。
3. 最终结果错误（扣2分）：由于上述错误累积，最终结果中出现了标准答案所没有的反正切项 \(-\frac{4}{\sqrt{3}}\arctan(\frac{2x+1}{\sqrt{3}})\)。在正确的分解下，对 \(\frac{2x+3}{x^2+x+1}\) 的积分可以直接得到 \(\ln(x^2+x+1)\)，无需也不应该出现反正切函数。这表明学生对有理函数分解后各项的积分方法掌握不牢。

尽管思路框架正确（想到用部分分式法），但由于核心的分解步骤错误，并导致了后续一系列连锁错误，最终答案不正确。根据打...