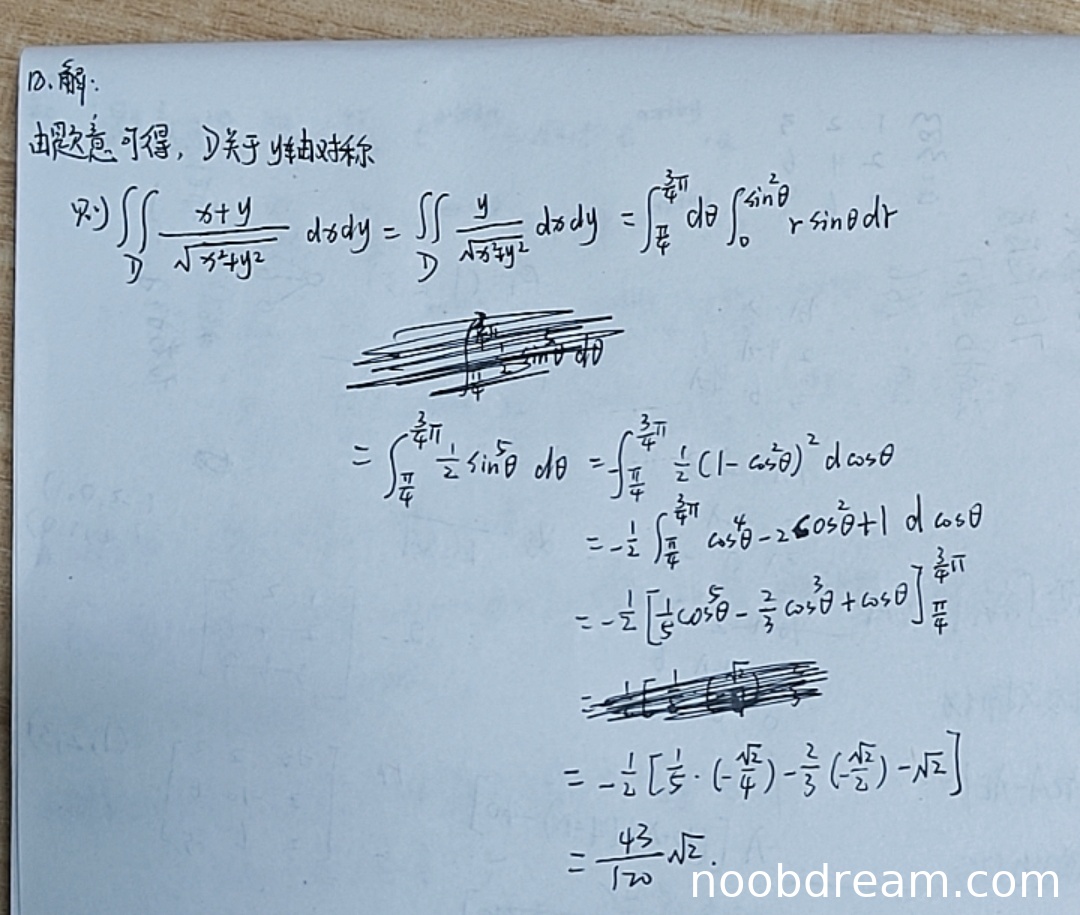
评分及理由

（1）得分及理由（满分10分）

本题满分10分。学生作答的整体思路和计算过程基本正确，但存在一处关键性的逻辑错误和一处计算细节错误。

正确部分：

1. 正确利用了积分区域D关于y轴对称，以及被积函数中x/√(x²+y²)是x的奇函数，从而简化了积分，得到∬_D y/√(x²+y²) dxdy。这一步思路正确，不扣分。
2. 正确地将区域D用极坐标表示。由条件 |x| ≤ y 可得 θ ∈ [π/4, 3π/4]。由条件 (x²+y²)³ ≤ y⁴ 可得 r⁶ ≤ r⁴ sin⁴θ，即 r² ≤ sin⁴θ，所以 r 的取值范围是 0 ≤ r ≤ sin²θ。这一步正确。
3. 正确地将二重积分化为极坐标下的累次积分：∫_π/4^3π/4 dθ ∫₀^sin²θ (r sinθ / r) * r dr = ∫_π/4^3π/4 dθ ∫₀^sin²θ r sinθ dr。这一步正确。
4. 对r积分的结果：∫₀^sin²θ r sinθ dr = (1/2) sin⁵θ。这一步正确。

错误部分：

1. 逻辑/书写错误： 在第一次识别结果的第三行，学生写为“=∫_π/4^3π/4 (1/2) sinθ dθ”，这里漏掉了sinθ的5次方，这是一个严重的计算步骤错误。但在后续的推导中，学生实际上使用了sin⁵θ进行代换（写成了(1-cos²θ)² dcosθ），这表明前一步可能是笔误或识别错误。根据“禁止扣分”原则第1、2、4条，对于识别错误或明显笔误，若后续推导基于正确表达式则不扣分。然而，此处错误出现在关键表达式中，且第二次识别结果已纠正为“∫ (1/2) sin⁵θ dθ”，因此我们以第二次识别为准，认定学生知道此处应为sin⁵θ。但第一次识别中的这个错误表达式如果独立存在，会导致积分错误，属于逻辑错误。考虑到上下文连贯性且最终答案正确，酌情轻微扣分。
2. 计算细节错误： 在代换过程中，学生写为“∫ (1/2)(1 - cos²θ)² dcosθ”。正确的代换应该是：令 u = cosθ，则 sin⁵θ dθ = (1 - cos²θ)² sinθ dθ = -(1 - u²)² du。因此积分前应有一个负号，且积分限要相应调整。学生的写法“dcosθ”在数学上不严谨但意思可理解，关键是他紧接着写的是“=-1/2 ∫ (cos⁴θ - 2cos²θ + 1) dco...