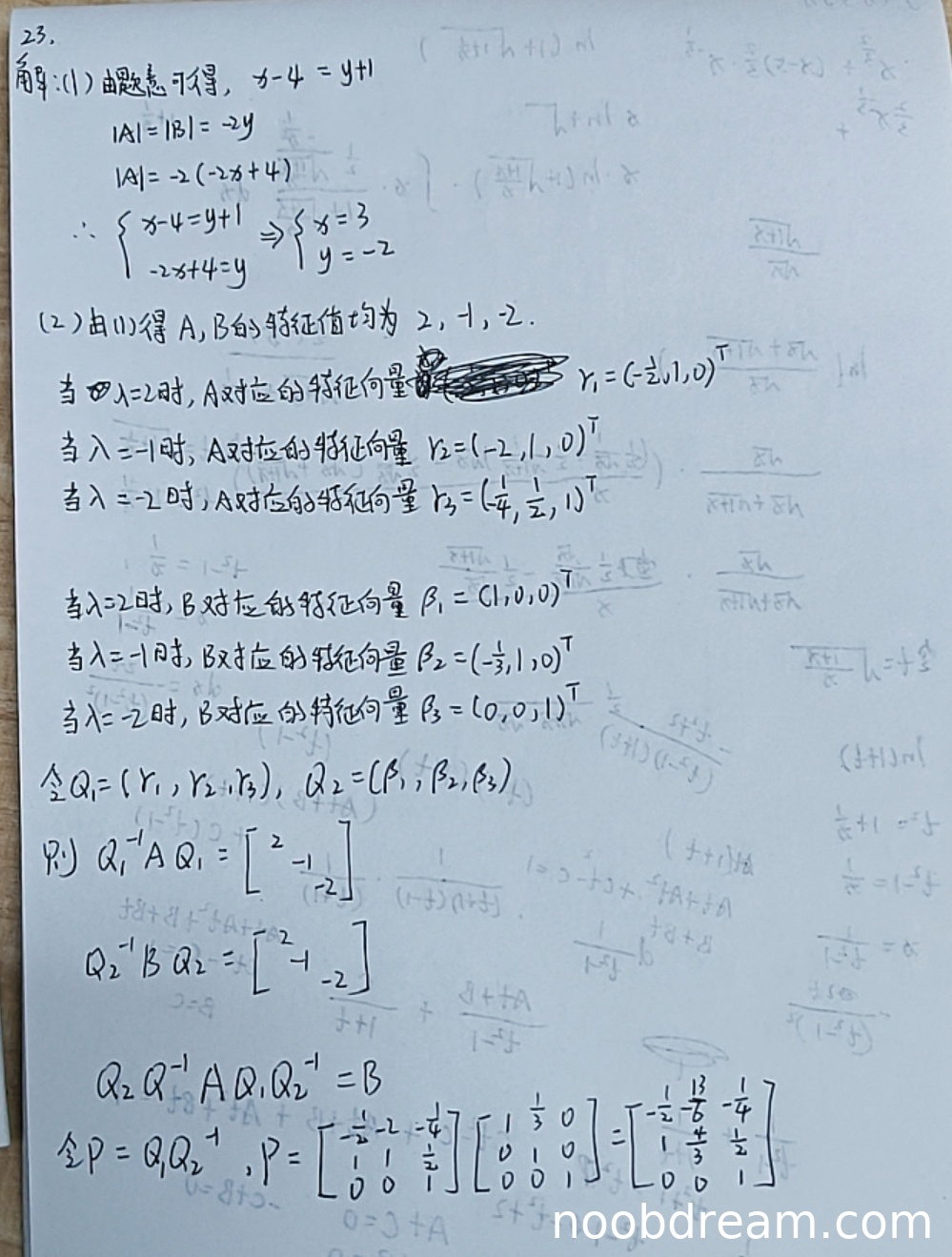
评分及理由

（Ⅰ）得分及理由（满分5分）

学生正确利用相似矩阵的性质：迹相等和行列式相等，建立方程组并解得 \(x=3, y=-2\)。思路正确，计算无误。但需注意，学生给出的第一个方程 \(x-4 = y+1\) 实际上是利用迹相等：\( \text{tr}(A) = -2+x+(-2) = x-4\)，\( \text{tr}(B) = 2+(-1)+y = y+1\)，因此 \(x-4 = y+1\) 正确。第二个方程利用行列式相等：\(|A| = -2(-2x+4) = 4x-8\)，\(|B| = -2y\)，因此 \(4x-8 = -2y\)，即 \(-2x+4 = y\)，与学生的写法一致。方程组解得正确。因此第(Ⅰ)部分得满分5分。

（Ⅱ）得分及理由（满分6分）

学生思路正确：先分别求A和B的特征值与特征向量，然后通过相似对角化构造过渡矩阵。但具体计算存在多处错误：

1. 对于矩阵A，当 \(\lambda=2\) 时，解 \((A-2I)x=0\)，学生给出的特征向量 \(\gamma_1 = (-\frac12, 1, 0)^T\) 是正确的（可验证）。
2. 当 \(\lambda=-1\) 时，解 \((A+I)x=0\)，学生给出 \(\gamma_2 = (-2, 1, 0)^T\)，但验证：\(A\gamma_2 = \begin{pmatrix}-2&-2&1\\2&3&-2\\0&0&-2\end{pmatrix}\begin{pmatrix}-2\\1\\0\end{pmatrix} = \begin{pmatrix}2\\-1\\0\end{pmatrix} = (-1)\begin{pmatrix}-2\\1\\0\end{pmatrix}\)，正确。
3. 当 \(\lambda=-2\) 时，解 \((A+2I)x=0\)，学生给出 \(\gamma_3 = (-\frac14, \frac12, 1)^T\)，验证：\(A\gamma_3 = \begin{pmatrix}-2&-2&1\\2&3&-2\\0&0&-2\end{pmatrix}\begin{pmatrix}-1/4\\1/2\\1\end{pmatrix} = \begin{pmatrix}1/2\\-1\\-2\end{pmatrix} = (-2)\b...