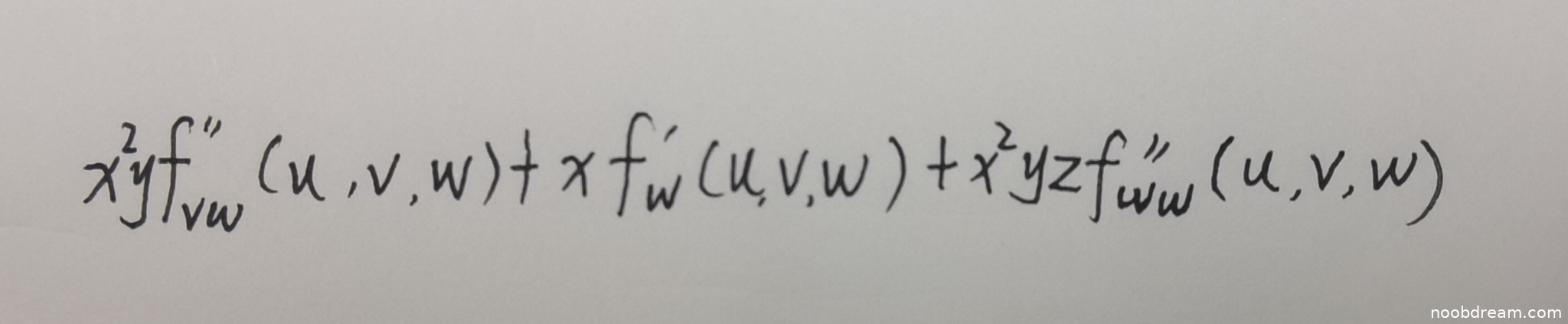
评分及理由

（1）得分及理由（满分5分）

学生两次识别结果分别为：
① \(x^{2}yf_{vw}''(u,v,w)+xf_{w}'(u,v,w)+x^{2}yzf_{www}''(u,v,w)\)
② \(x^{2}yf_{vw}''(u,v,w)+xf_{w}'(u,v,w)+x^{2}yzf_{ww}''(u,v,w)\)

标准答案为：\( x f'_{3} + x^{2} y f''_{32} + x^{2} y z f''_{33} \)。

对比分析：
1. 符号对应关系：在题目设定的函数 \( f(u, v, w) \) 中，标准答案的下标 1, 2, 3 分别对应第一、第二、第三个中间变量，即 \( u, v, w \)。因此： - \( f'_{3} \) 对应 \( f'_w \) 或 \( f_w' \)。 - \( f''_{32} \) 对应 \( f''_{wv} \) 或 \( f_{vw}'' \)（二阶连续偏导次序可交换）。 - \( f''_{33} \) 对应 \( f''_{ww} \) 或 \( f_{ww}'' \)。

2. 学生答案与标准答案的匹配： - 第一项：学生的 \( xf_{w}'(u,v,w) \) 对应标准答案的 \( x f'_{3} \)，正确。 - 第二项：学生的 \( x^{2}yf_{vw}''(u,v,w) \) 对应标准答案的 \( x^{2} y f''_{32} \)，正确。 - 第三项：学生的第二次识别结果 \( x^{2}yzf_{ww}''(u,v,w) \) 对应标准答案的 \( x^{2} y z f''_{33} \)，正确。第一次识别结果中的 \( f_{www}'' \) 显然是识别错误（多了一个w），但根据“两次识别只要有一次正确则不扣分”的规则，以及上下文可判断为误写，不扣分。

因此，学生的答案（以第二次识别为准）在数学本质上与标准答案完全一致，只是偏导数记号写法不同（下标数字与字母的对应、偏导符号位置），这属于等价表达，思路和结果均正确。

根据评分要求，思路正确不扣分，识别误写不扣分，答案正确给满分。

得分：5分

题目总分：5分