评分及理由

（1）得分及理由（满分3分）

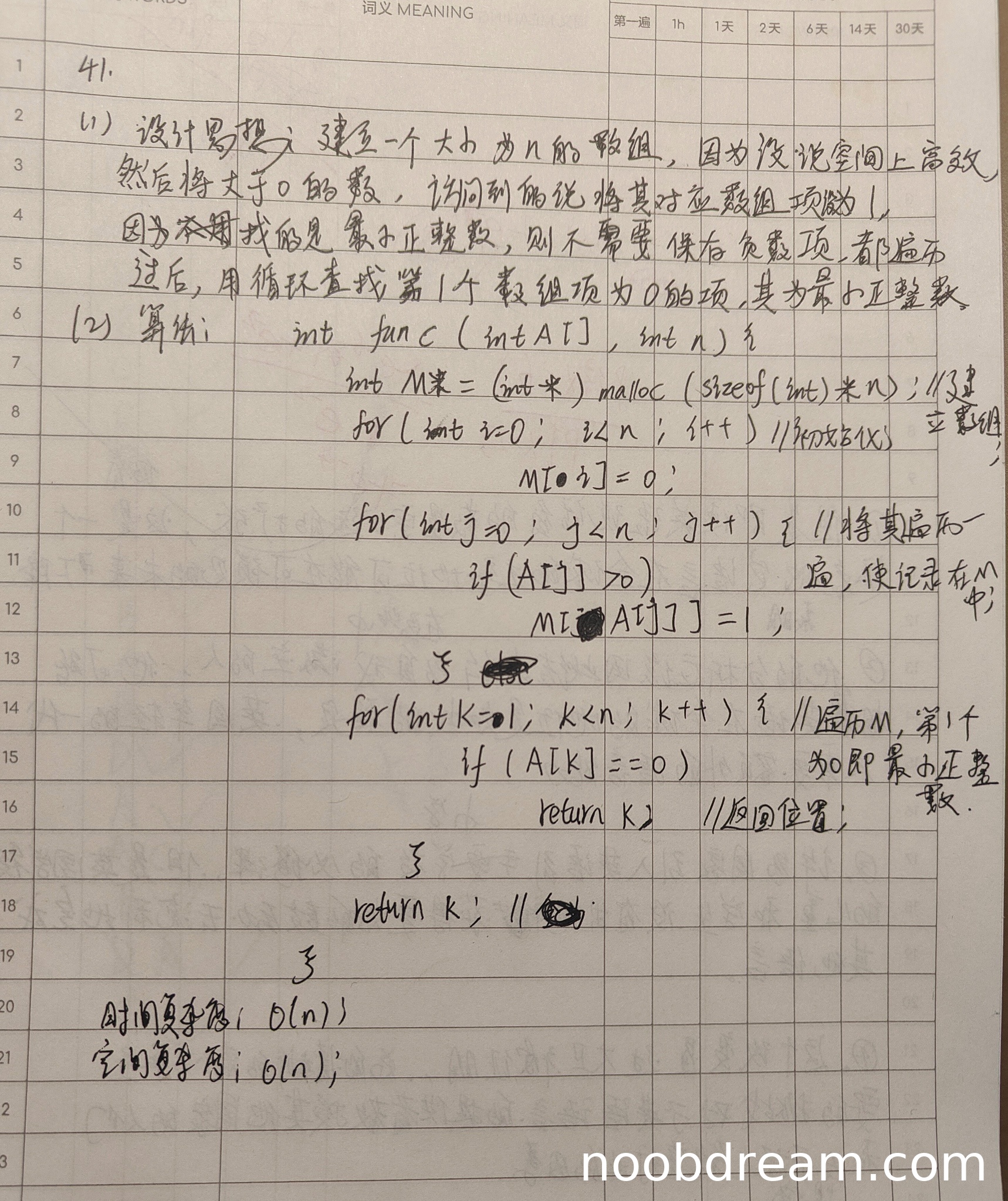
学生设计思路是建立一个大小为n的辅助数组M，用于标记正整数是否出现。思路基本正确，能够解决问题。但存在以下问题：
1. 辅助数组M的大小为n，而数组A中的正整数可能大于n，直接使用M[A[j]] = 1会导致数组越界（例如A[j]=n时，M[n]越界）。标准答案通过将大于n的数忽略或处理来避免越界，而学生答案未考虑此点，属于逻辑缺陷。
2. 思路描述中“因为要找的是最小正整数，则不需要保存负数项”是正确的，但未处理非正整数（0和负数）以及大于n的数，导致标记数组可能越界或遗漏。
由于思路存在越界风险，但整体方向正确，扣1分。
得分：2分

（2）得分及理由（满分8分）

学生代码实现了设计思路，但存在多处逻辑错误：
1. 在第一个识别结果中，第三个循环判断条件if (A[k] == 0)错误，应为判断M数组；第二个识别结果已修正为if (M[k] == 0)，但根据“两次识别只要有一次正确则不扣分”原则，此处不扣分。
2. 辅助数组M的大小为n，但下标访问M[A[j]]中，若A[j]等于n则越界（因为M下标范围为0到n-1）。例如n=4，A[j]=4时，M[4]越界。标准答案通过限制num≤n来避免。
3. 第三个循环从k=1开始，但若最小正整数是n+1（如数组{1,2,3}），则循环不会返回正确结果，应返回n+1。学生代码最后返回k，但此时k=n，且未处理n+1的情况。
4. 代码未释放malloc分配的内存，但题目未要求，不扣分。
由于核心逻辑存在数组越界风险和未处理n+1情况，扣4分。
得分：4分

（3）得分及理由（满分2分）

学生正确给出了时间复杂度O(n)和空间复杂度O(n)，与算法一致。
得分：2分

题目总分：2+4+2=8分