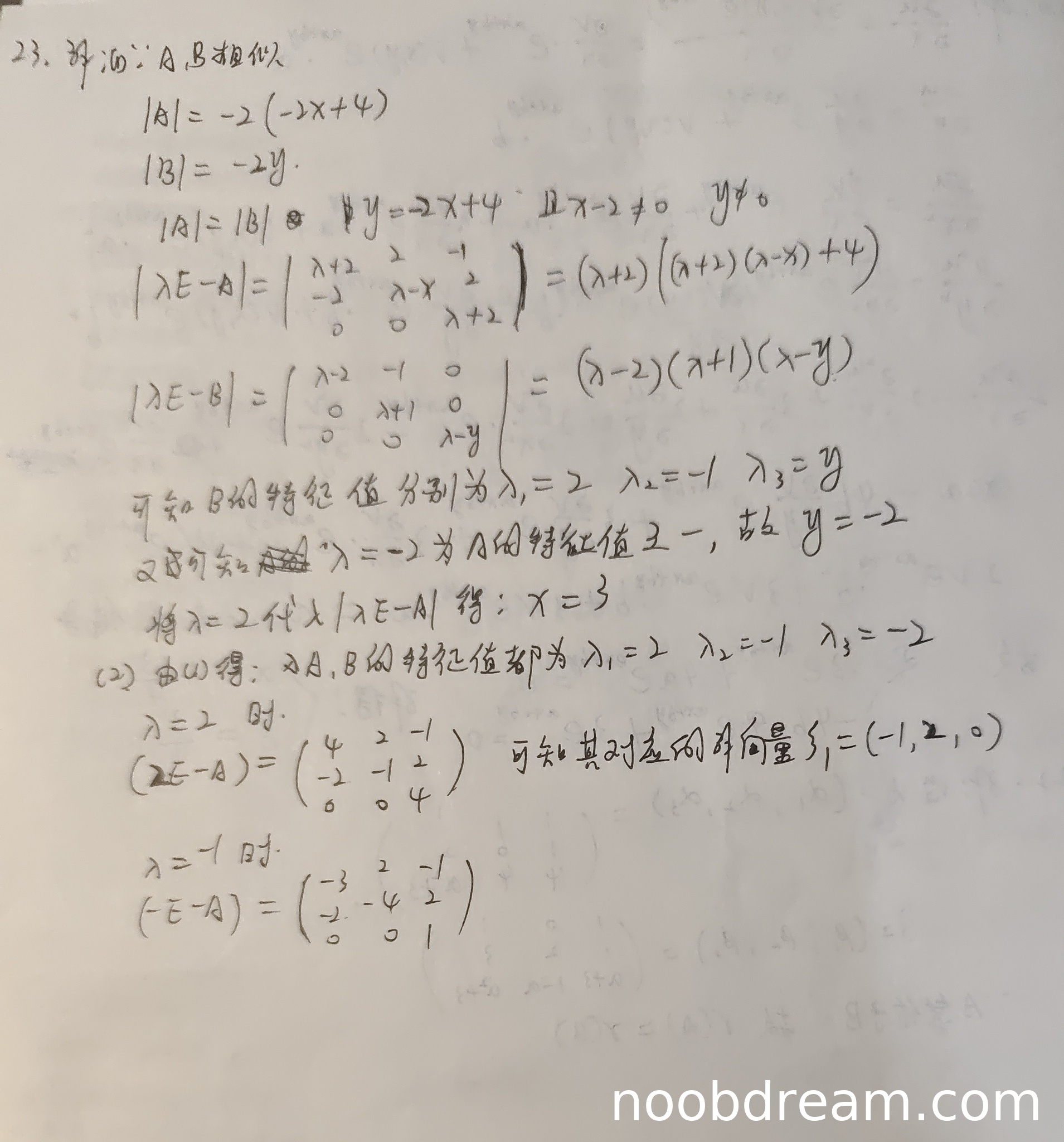
评分及理由

（Ⅰ）得分及理由（满分5分）

学生首先利用相似矩阵行列式相等得到 |A| = |B|，但计算 |A| 时出现错误：|A| = -2*(-2x - (-2)*2?) 正确计算应为 |A| = (-2)*[x*(-2) - (-2)*2] - (-2)*[2*(-2)-0] + 1*[2*0-0] = (-2)(-2x+4) = 4x-8。而学生写成了 -2(-2x+4) = 4x-8，但后续等式处理时误写为 y = -2x+4（实际上由 |A|=4x-8, |B|=-2y，得 4x-8=-2y ⇒ y = -2x+4，这一步正确）。不过后面从特征多项式入手，发现 λ=-2 是 A 的特征值（因为矩阵 A 是上三角？实际上 A 的第三行是 (0,0,-2)，所以 -2 是特征值），由相似矩阵特征值相同，得到 y=-2，再代入 y=-2x+4 得 x=3。虽然中间行列式计算表述有小瑕疵，但最终结果正确，且核心逻辑（用特征值相等求 y，再代入行列式相等求 x）正确。因此扣 1 分（行列式推导表述有误，但不影响最终答案）。得 4 分。

（Ⅱ）得分及理由（满分6分）

学生只给出了 λ=2 的特征向量 ξ₁=(-1,2,0)，并写出了 λ=-1 对应的矩阵 (-E-A)，但没有完整解出三个线性无关的特征向量，也没有构造出矩阵 P。题目要求是求出可逆矩阵 P 使得 P⁻¹AP=B，因此必须给出完整的 P。学生作答未完成，只能得到部分分数。考虑到（Ⅱ）需要基于（Ⅰ）的结果，且学生有求解特征向量的思路，但未完成全部计算，给 2 分。

题目总分：4+2=6分