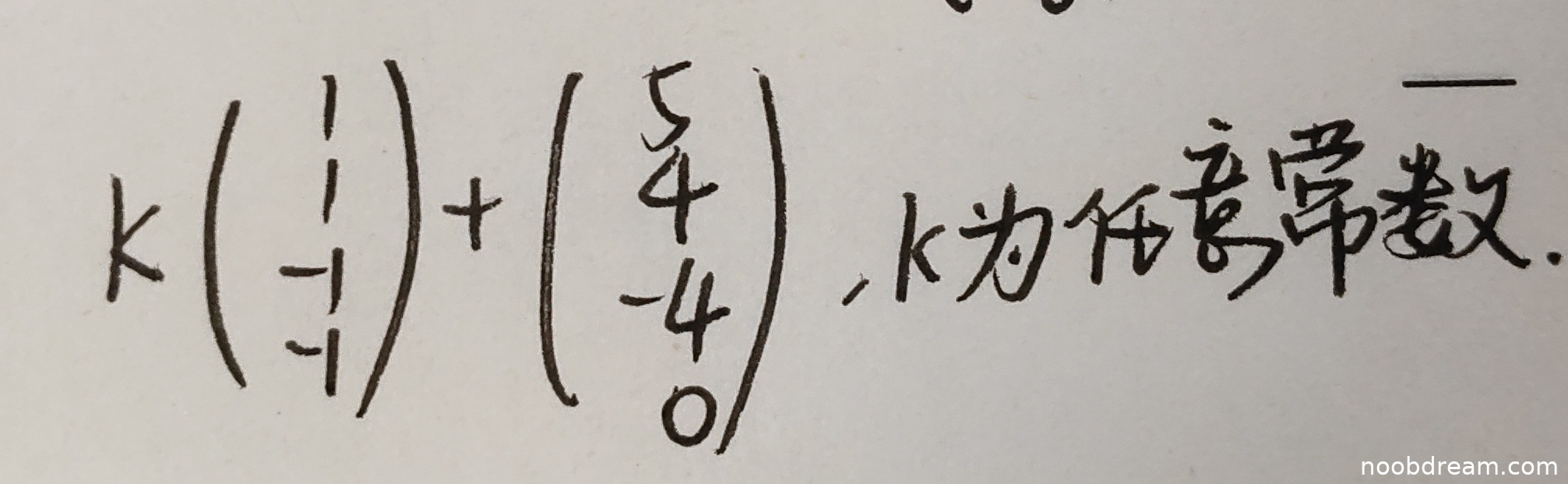
评分及理由

（1）得分及理由（满分5分）

本题为填空题，标准答案为 \(k\begin{pmatrix}1\\1\\ - 1\\ - 1\end{pmatrix}+\begin{pmatrix}1\\0\\0\\4\end{pmatrix}\)，其中 \(k\) 为任意常数。

学生第一次识别结果为：\(k\begin{pmatrix}1\\1\\-1\\-1\end{pmatrix}+\begin{pmatrix}5\\4\\-4\\0\end{pmatrix}\)。

学生第二次识别结果为：$k\begin{pmatrix}1\\1\\ - 1\\-1\end{pmatrix}+\begin{pmatrix}5\\4\\4\\ - 4\\0\end{pmatrix},k为任意常数.$（第二个向量维度错误，可能为识别问题）

分析：

1. 齐次解部分：学生答案的齐次解部分为 \(\begin{pmatrix}1\\1\\-1\\-1\end{pmatrix}\)，这与标准答案一致。该向量由条件 \(a_1 + a_2 = a_3 + a_4\) 可得 \(a_1 + a_2 - a_3 - a_4 = 0\)，即 \(x = (1, 1, -1, -1)^T\) 是齐次方程 \(Ax=0\) 的一个非零解。由于 \(a_1, a_2, a_3\) 线性无关，且 \(a_4\) 可由它们线性表示（由 \(a_1 + a_2 - a_3 = a_4\)），故矩阵 \(A\) 的秩为3，齐次解空间维数为1。因此齐次通解部分正确。
2. 特解部分：学生答案的特解为 \(\begin{pmatrix}5\\4\\-4\\0\end{pmatrix}\)（以第一次识别为准）。我们需要检验 \(A \begin{pmatrix}5\\4\\-4\\0\end{pmatrix} = a_1 + 4a_4\) 是否成立。
   • 由已知 \(a_1 + a_2 = a_3 + a_4\)，可得 \(a_4 = a_1 + a_2 - a_3\)。
   • 计算 \(A \begin{pmatrix}5\\4\\-4\\0\end{pmatrix} = 5a_1 + 4a_2 - 4a_3 + 0 \cdot a_4 = 5a_1 + 4a_2 - 4a_3\...