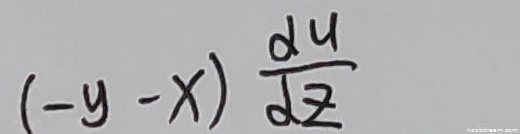
评分及理由

（1）得分及理由（满分5分）

学生答案为：\((-y - x)\frac{du}{dz}\)。

标准答案为：\(f_{1}'+f_{2}'-(x+y)f_{3}'\)。

分析：题目要求计算 \(\frac {\partial u}{\partial x}+\frac {\partial u}{\partial y}\)。学生答案的表达式 \((-y - x)\frac{du}{dz}\) 存在以下问题：

1. 符号表示错误：学生使用了常微分符号 \(\frac{du}{dz}\)，但 \(u\) 是 \(x, y, z\) 的函数，而 \(z\) 又是 \(x, y\) 的函数，因此这里应是偏导数 \(\frac{\partial u}{\partial z}\) 或 \(f_3'\)。使用 \(\frac{du}{dz}\) 在多元函数链式法则的上下文中是不规范的，且可能暗示对 \(z\) 的全导数，这与题意不符。
2. 缺失关键项：根据链式法则，\(\frac{\partial u}{\partial x} = f_1' + f_3' \cdot \frac{\partial z}{\partial x}\)，\(\frac{\partial u}{\partial y} = f_2' + f_3' \cdot \frac{\partial z}{\partial y}\)。因此，\(\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y} = f_1' + f_2' + f_3' \cdot (\frac{\partial z}{\partial x} + \frac{\partial z}{\partial y})\)。学生答案仅给出了 \(f_3'\) 乘以一个系数的形式，完全缺失了 \(f_1'\) 和 \(f_2'\) 项。
3. 系数可能来源：学生答案中的系数 \((-y-x)\) 与标准答案中 \(-(x+y)\) 在数值上相等。这可能是学生正确地从隐函数方程 \(\int_{0}^{xy+z}e^{-t^{2}}dt=1\) 求出了 \(\frac{\partial z}{\partial x} = -y\) 和 \(\frac{\partial z}{\part...