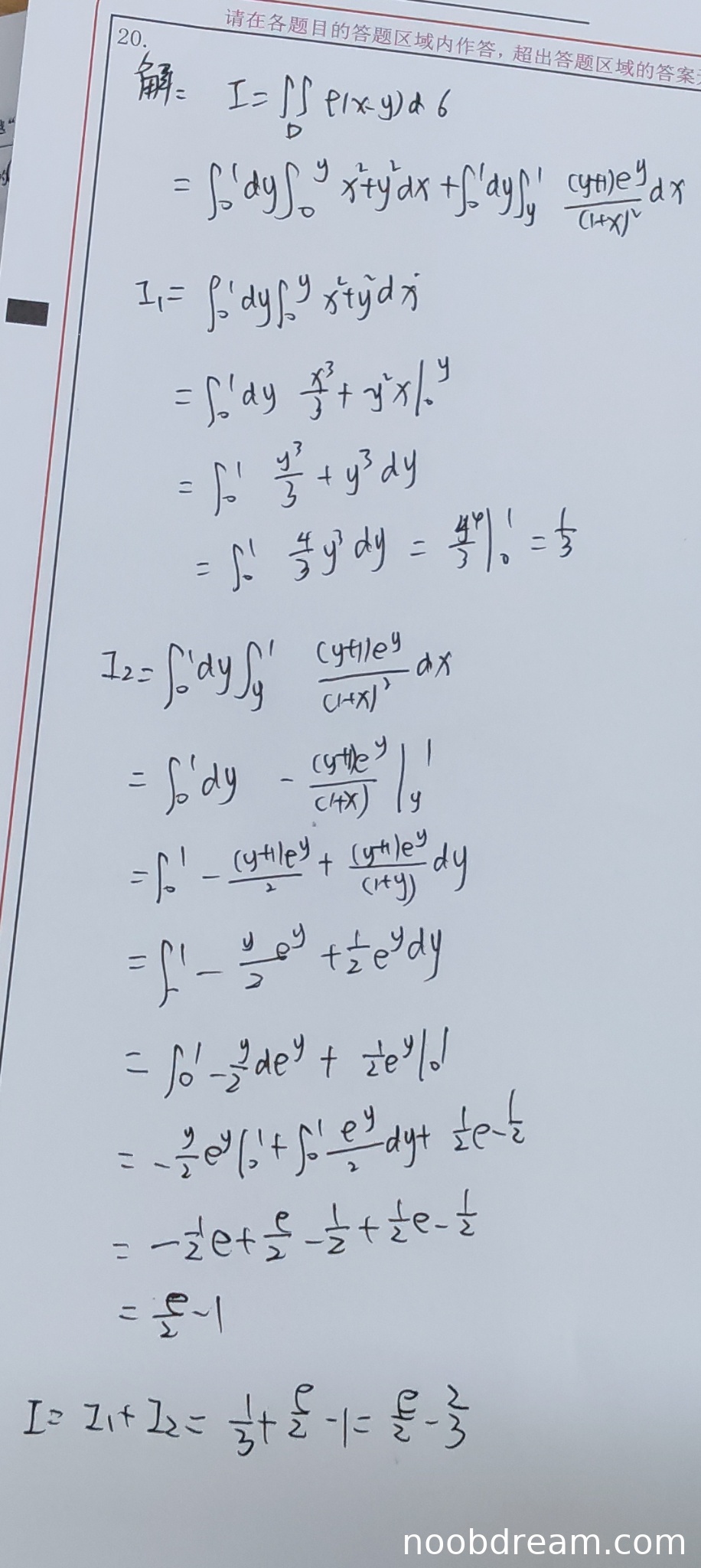
评分及理由

（1）得分及理由（满分12分）

学生作答给出了两次识别结果，但核心内容一致。整体思路正确：将区域D按y=x分割为两部分，分别对应被积函数的不同表达式，然后化为二次积分计算。

具体步骤：
1. 正确写出积分区域的分割方式，并对应正确的被积函数。
2. 计算 \(I_1 = \iint_{D_2} (x^2+y^2)d\sigma\) 时，积分次序选择先x后y（x从0到y，y从0到1），计算过程正确，结果 \(\frac{1}{3}\) 正确。
3. 计算 \(I_2 = \iint_{D_1} \frac{(y+1)e^y}{(1+x)^2}d\sigma\) 时，积分次序选择先x后y（x从y到1，y从0到1）。这里需要注意，学生第一次识别结果中写的是 \(\int_{0}^{1}dy\int_{y}^{1} \frac{(y+1)e^{y}}{(1+x)^{2}}dx\)，这对应的是区域 \(D_1\)（即y 4. 最终求和得到 \(\frac{e}{2}-\frac{2}{3}\)，与标准答案一致。

尽管第二次识别结果中 \(I_1\) 的积分表达式出现了笔误（写成了 \(\int_{0}^{1}dy\int_{0}^{y}\frac{x^{2}}{x + y}dx\)），但根据上下文（后续计算步骤和结果）可以判断为识别错误，且第一次识别结果中该部分表达式正确。根据“禁止扣分”原则，此类识别错误不扣分。

因此，该解答逻辑清晰，计算正确，应得满分。

得分：12分

题目总分：12分