2026年李林冲刺预测6套卷（一） - 第14题回答

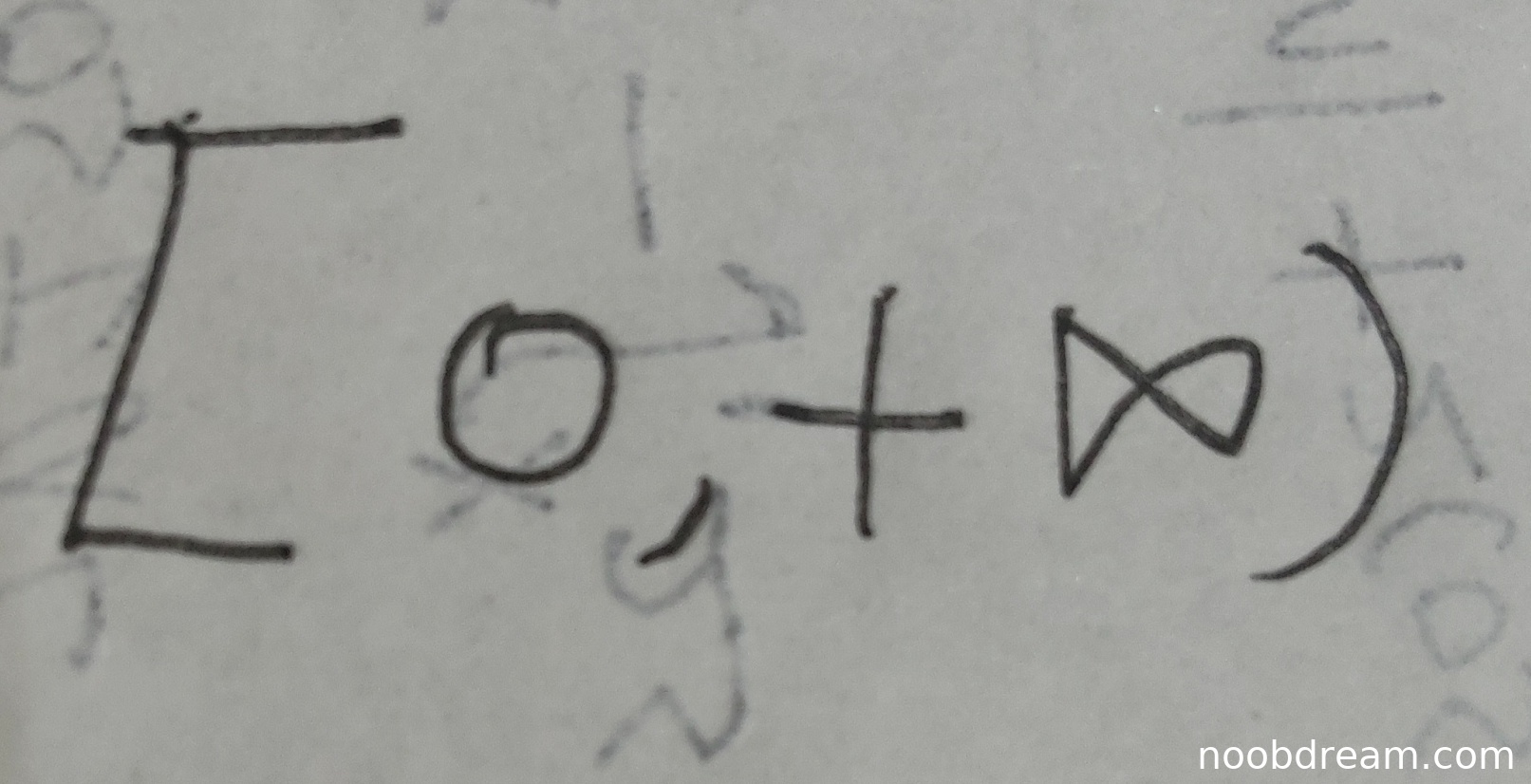
好的，我们先一步步分析。 --- **1. 题目分析** 题目是二阶常系数齐次线性微分方程 \[ y'' + a y' + y = 0 \] 特征方程： \[ r^2 + a r + 1 = 0 \] 特征根： \[ r = \frac{-a \pm \sqrt{a^2 - 4}}{2} \] 要求：**每一个解** \(y(x)\) 在 \([0, +\infty)\) 上有界。 --- **2. 有界性条件** - 当 \(a^2 - 4 > 0\)（即 \(|a| > 2\)）时，两根为实根 \(r_1, r_2\)。 解有界要求两根非正（若为正则指数增长无界）。 两根之和 \(r_1 + r_2 = -a\)，积 \(r_1 r_2 = 1 > 0\)，所以两根同号。 积为正且和为负 ⇒ 两根均为负实数 ⇒ 此时解有界。 条件：\(a > 2\)（因为若 \(a < -2\)，则两根均为负？检查：若 \(a = -3\)，则 \(r^2 - 3r + 1 = 0\)，根为 \((3 \pm \sqrt{5})/2 > 0\)，正根 ⇒ 无界。所以必须 \(a > 2\) 才保证两根均为负。） 仔细算： 两根同号且积=1 ⇒ 同为正或同为负。 若同为负，则 \(r_1 + r_2 = -a < 0\) ⇒ \(a > 0\)。 在 \(a > 0\) 且 \(a^2 > 4\) ⇒ \(a > 2\) 时，两根为负实根，有界。 - 当 \(a^2 - 4 = 0\)（即 \(a = \pm 2\)）时： \(a = 2\)：\(r = -1\)（重根），解 \(y = (c_1 + c_2 x)e^{-x}\)，当 \(x \to +\infty\) 时趋于 0，有界。 \(a = -2\)：\(r = 1\)（重根），解 \(y = (c_1 + c_2 x)e^{x}\)，无界。 - 当 \(a^2 - 4 < 0\)（即 \(|a| < 2\)）时： 两根为共轭复根：实部为 \(-a/2\)。 解有界 ⇔ 实部 ≤ 0 ⇔ \(-a/2 \le 0\) ⇔ \(a \ge 0\)。 结合 \(|a| < 2\) 且 \(a \ge 0\) ⇒ \(0 \le a < 2\) 时有界。 --- **3. 合并条件** (1) \(a > 2\)：负实根，有界 ✅ (2) \(a = 2\)：重根 -1，有界 ✅ (3) \(0 \le a < 2\)：复根实部 ≤ 0，有界 ✅ (4) \(a < 0\) 时： - 若 \(-2 < a < 0\)，复根实部 > 0 ⇒ 无界 ❌ - 若 \(a = -2\)，重根 1 ⇒ 无界 ❌ - 若 \(a < -2\)，两根一正一负（积=1>0，和=-a>0 ⇒ 两根均为正）⇒ 无界 ❌ 因此 **所有解有界的充要条件是 \(a \ge 0\)**。 --- **4. 标准答案** 标...

赞同