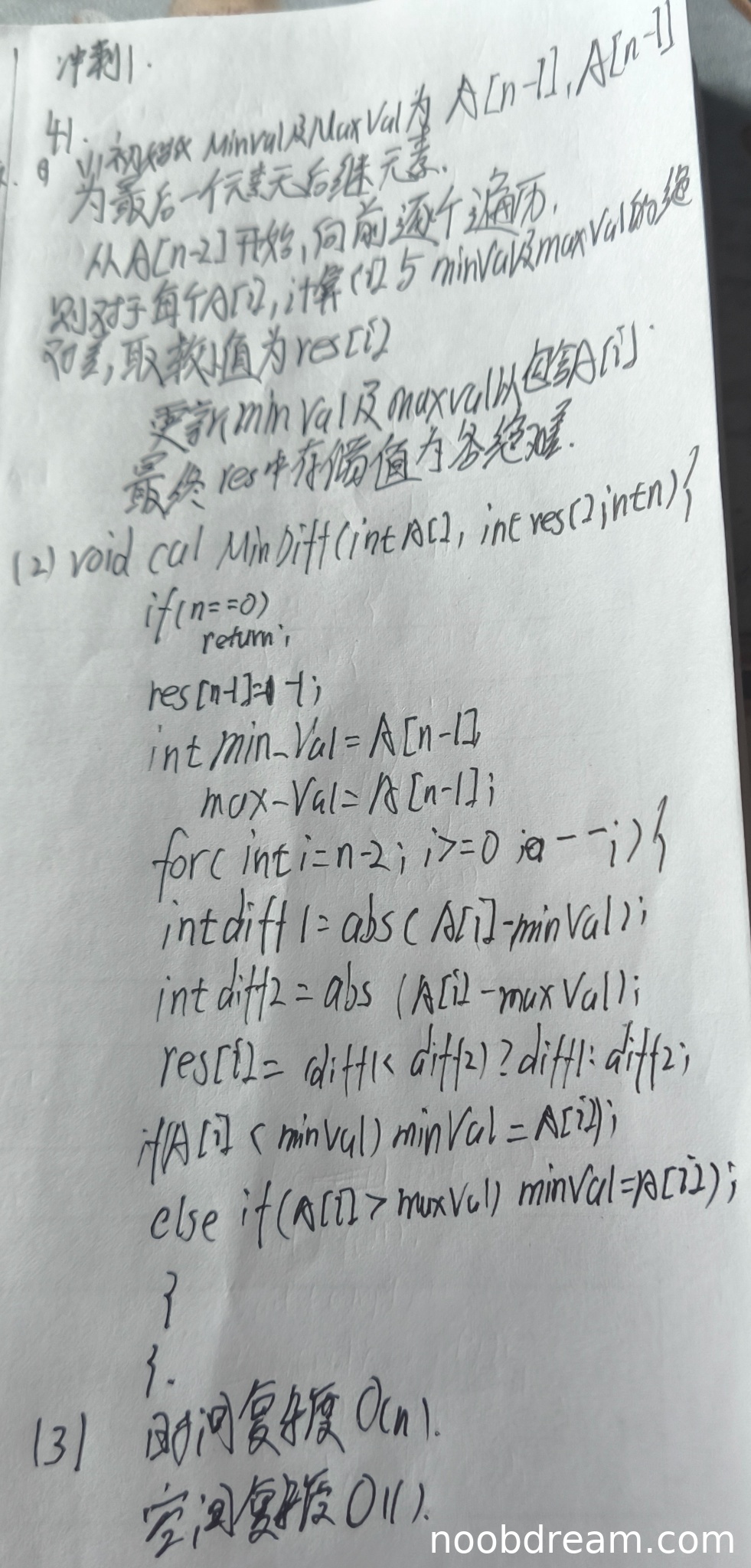
评分及理由

（1）得分及理由（满分4分）

得分：0分

理由：学生的算法设计思想存在根本性错误。其核心思路是仅维护已遍历元素的最小值（min_Val）和最大值（max_Val），并认为对于当前元素A[i]，它与后续所有元素的最小绝对差，必然是与这个最小值或最大值的绝对差之一。这是不正确的。例如，数组A = [5, 8, 4, 7]，从右向左处理，当i=0时，A[0]=5，已遍历元素为[8,4,7]，其min_Val=4，max_Val=8。按照学生算法，res[0] = min(|5-4|, |5-8|) = 1。但实际上，A[0]与后续元素的最小绝对差是与A[3]=7的差，即|5-7|=2，而1是与A[2]=4的差，但A[2]的索引2 > 0，它确实是后续元素，所以这里学生算法碰巧得到了正确结果。然而，考虑另一个例子A = [10, 2, 1, 12]，从右向左，当i=0时，A[0]=10，已遍历元素为[2,1,12]，min_Val=1，max_Val=12。学生算法给出res[0] = min(|10-1|, |10-12|) = 2。但实际最小绝对差是|10-12|=2，这里又碰巧对了。但关键反例：A = [5, 3, 8, 6]。从右向左，处理A[0]=5时，后续元素[3,8,6]，min_Val=3，max_Val=8。学生算法给出res[0] = min(|5-3|, |5-8|) = 2。但实际最小绝对差是|5-6|=1。因此，该设计思想不能保证结果的正确性，属于逻辑错误。故本部分不得分。

（2）得分及理由（满分7分）

得分：0分

理由：代码是算法思想的直接实现。由于算法设计思想存在根本逻辑错误（如上所述），导致代码无法在所有情况下计算出正确的结果。代码本身语法正确，且实现了从右向左扫描并更新min_Val和max_Val的逻辑，但因其核心算法错误，故不能得分。

（3）得分及理由（满分2分）

得分：0分

理由：学生分析其算法的时间复杂度为O(n)，空间复杂度为O(1)。这个分析是基于其错误算法得出的。虽然对于其错误的算法而言，复杂度分析本身是正确的，但题目要求的是“说明你所设计算法的时间复杂度和空间复杂度”，而该算法因逻辑错误未能正确解决问题，因此其复杂度分析失去了意义，不予给分。

题目总分：0+0+0=0分