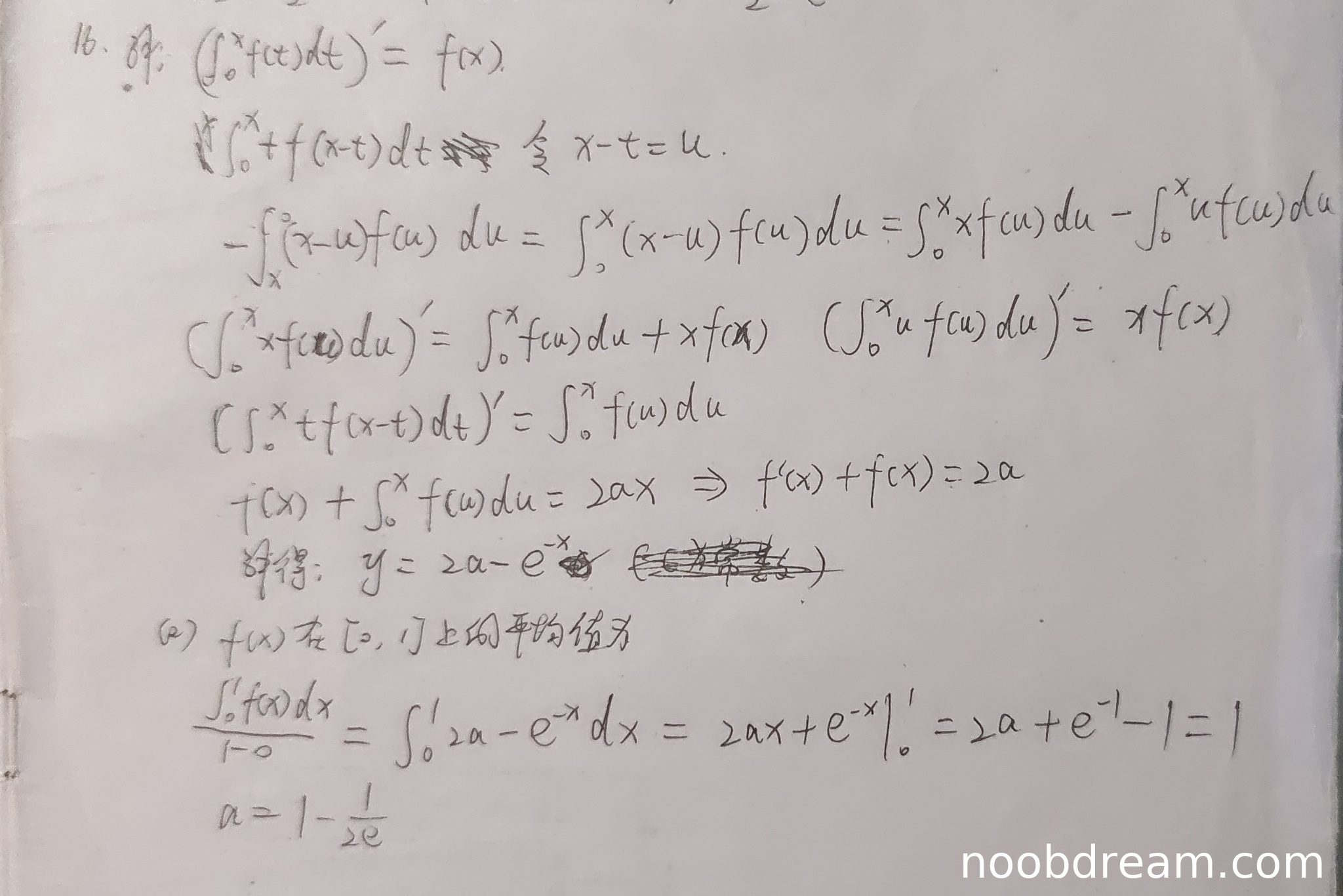
评分及理由

（I）得分及理由（满分5分）

学生作答在第一次识别中，对积分 \(\int_{0}^{x} t f(x-t) dt\) 的变量代换处理有误（写成了 \(\int_{0}^{x} f(x-t) dt\)，漏掉了因子 \(t\)），导致后续求导结果出现偏差。但第二次识别给出了正确的变量代换过程：\(\int_{0}^{x} t f(x-t) dt = \int_{0}^{x} (x-u) f(u) du = x\int_{0}^{x} f(u) du - \int_{0}^{x} u f(u) du\)。代入原方程后得到： \[ \int_{0}^{x} f(t) dt + x\int_{0}^{x} f(u) du - \int_{0}^{x} u f(u) du = a x^2 \] 两边对 \(x\) 求导，利用乘积法则和变上限积分求导，得到： \[ f(x) + \int_{0}^{x} f(u) du + x f(x) - x f(x) = 2a x \] 即 \[ f(x) + \int_{0}^{x} f(u) du = 2a x \] 再求导得： \[ f'(x) + f(x) = 2a \] 这是一阶线性微分方程，解得通解为 \(f(x) = 2a + C e^{-x}\)。利用初始条件（令原方程中 \(x=0\) 可得 \(f(0)=0\)）得 \(C = -2a\)，所以 \(f(x) = 2a - 2a e^{-x}\)。

学生第二次识别的求解过程中，在得到通解 \(f(x)=2a+Ce^{-x}\) 后，代入初始条件时误写为 \(C=-2a\) 但结果却写成了 \(f(x)=2a - e^{-x}\)（漏了系数 \(2a\) 在指数项前），这属于计算错误。因此，虽然思路基本正确，但最终表达式有误。

扣分：思路正确（变量代换、建立微分方程、求解）可得大部分分数，但最终结果错误，扣2分。

得分：3分（满分5分）

（II）得分及理由（满分5分）

根据（I）中得到的错误表达式 \(f(x)=2a - e^{-x}\)，学生计算了积分： \[ \int_0^1 (2a - e^{-x}) dx = \left[2ax + e^{-x}\right]_0^1 = 2a + e^{-1} - 1 \] 令其等于1（因为平均值为1），...