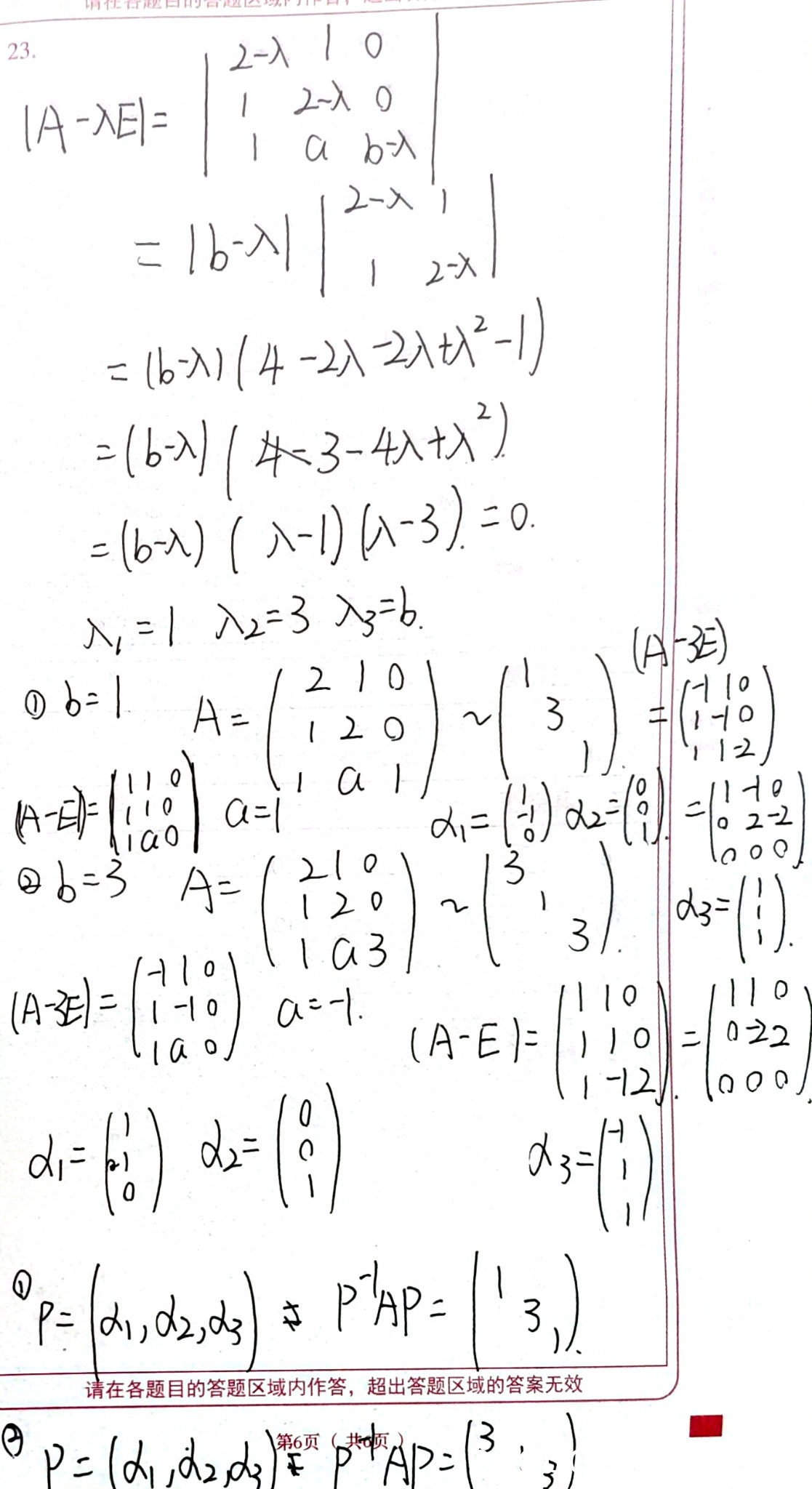
评分及理由

（1）特征值计算部分（满分3分）

学生正确计算了特征多项式，得到特征值为 λ₁=1, λ₂=3, λ₃=b。此部分逻辑完整，计算无误。得3分。

（2）分情况讨论参数 a, b 的值（满分4分）

学生正确分两种情况讨论：b=1 和 b=3。在每种情况下，都正确运用了矩阵可相似对角化的条件（即几何重数等于代数重数，通过秩的条件体现），并分别求出对应的 a 值（a=1 和 a=-1）。思路和结果均正确。得4分。

（3）求可逆矩阵 P 及对角矩阵（满分5分）

学生给出了两种情况下特征向量的求解思路和结果，并指出 P 由特征向量构成，P⁻¹AP 为对角阵。但在具体表述和最终结果的对角矩阵元素排列上存在一些混乱和笔误（例如第一次识别结果中，对角矩阵的写法不规范且有明显错误；第二次识别结果中，b=3 情况下的特征向量 α₁, α₂ 与标准答案不同，且对角矩阵的写法也不规范）。这些属于表述和细节错误，但核心逻辑（用特征向量构造 P）是正确的。考虑到题目要求“求可逆矩阵 P，使 P⁻¹AP 为对角矩阵”，学生给出了正确的构造方法和特征向量（尽管第二次识别中 b=3 时的 α₂ 与标准答案不同，但计算出的向量 (-1,0,1)ᵀ 确实是 (E-A)x=0 的解，是有效的特征向量，可以构成 P），因此扣1分。得4分。

题目总分：3+4+4=11分