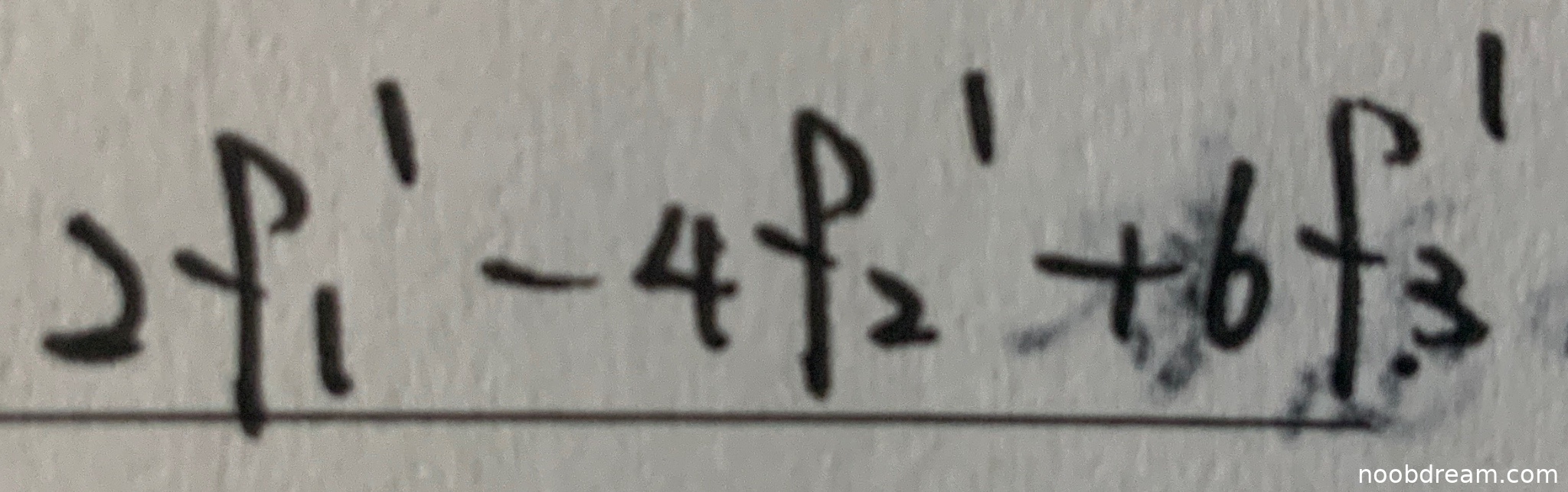
评分及理由

（1）得分及理由（满分5分）

学生答案为：$2f_{1}'-4f_{2}'+6f_{3}'$。标准答案为：$2f_{1}'(1,2,1)-8f_{2}'(1,2,1)+9f_{3}'(1,2,1)$。

对比分析：

1. 核心思路判断：题目要求计算复合函数 $\frac{du}{dx}$ 在 $x=1$ 处的值。学生答案包含了 $f_1', f_2', f_3'$ 的线性组合，这表明学生掌握了链式法则的基本思想，即 $du/dx$ 应表达为 $f$ 对各中间变量的偏导数与这些中间变量对 $x$ 的导数的乘积之和。思路方向正确。
2. 具体数值错误：学生答案中 $f_2'$ 和 $f_3'$ 的系数（分别为 -4 和 6）与标准答案（分别为 -8 和 9）不符。同时，学生答案中偏导数 $f_i'$ 后缺少了在具体点 $(1,2,1)$ 的取值标注。这表明学生在计算中间变量 $x^2, 2y, z^3$ 在 $x=1$ 处对 $x$ 的导数时，或者在求解 $y'(1)$ 和 $z'(1)$ 时出现了计算错误。
3. 扣分依据：根据打分要求第2条“逻辑错误扣分”，此处的数值计算错误属于逻辑推导或计算过程中的错误，导致最终答案不正确。因此不能给满分。根据第5条“计算题目总分时，对于有逻辑错误的答案不要给满分”，本题应扣分。
4. 分数判定：由于答案的核心形式（三个偏导数的线性组合）正确，但具体系数全部错误，且缺少关键点的标注，属于部分正确但存在重大计算失误。在填空题的严格评判下（正确则5分，错误则0分），此答案与标准答案不完全一致，应判定为错误。因此得分为0分。

题目总分：0分