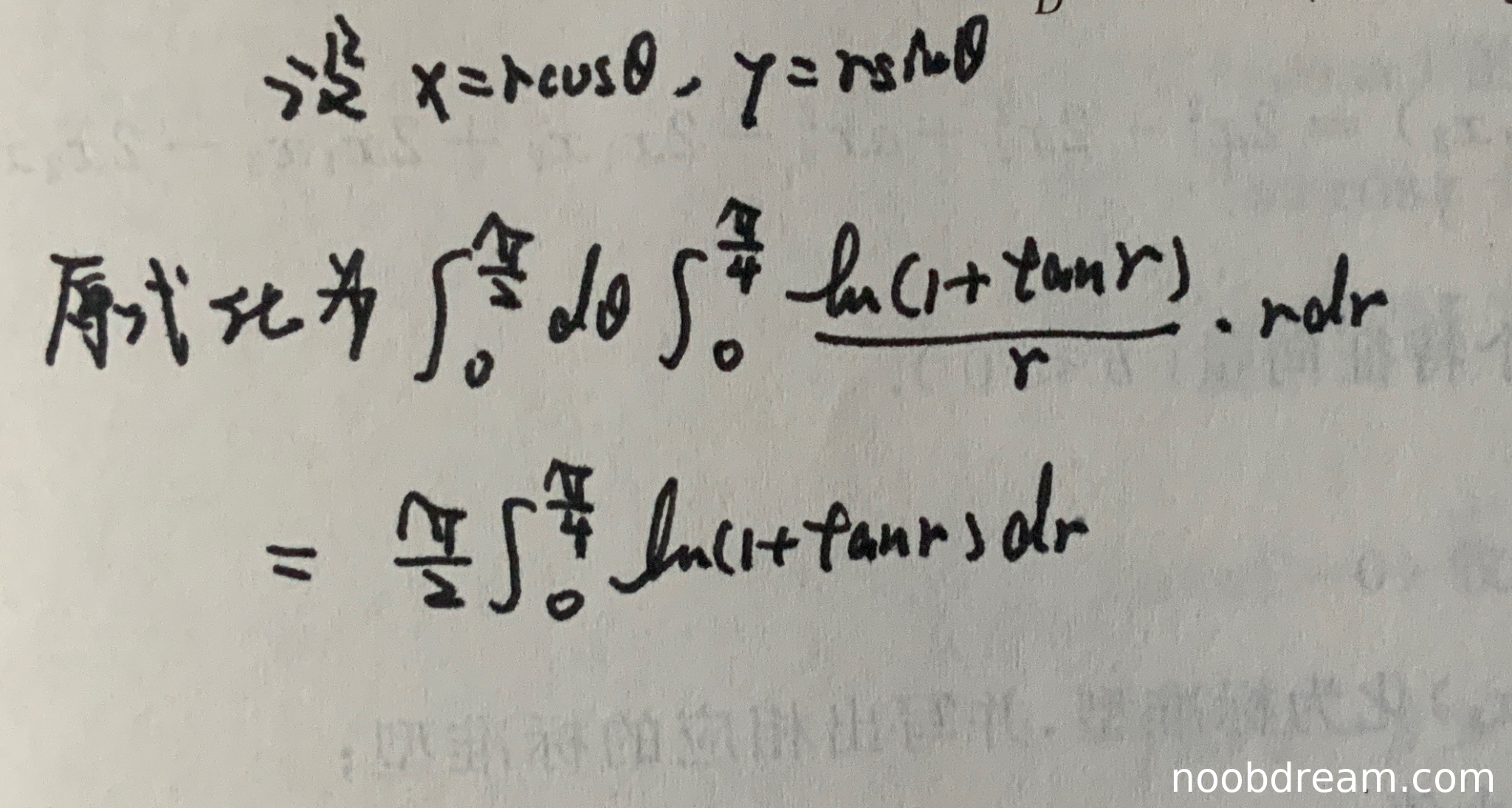
评分及理由

（1）得分及理由（满分12分）

学生作答给出了从直角坐标到极坐标的换元过程，并正确地将积分区域转化为极坐标下的积分限：\( \theta \) 从 \( 0 \) 到 \( \frac{\pi}{2} \)，\( r \) 从 \( 0 \) 到 \( \frac{\pi}{4} \)。被积函数也正确地转换为 \( \frac{\ln(1+\tan r)}{r} \cdot r \)，并化简为 \( \ln(1+\tan r) \)。计算得到 \( \frac{\pi}{2} \int_{0}^{\frac{\pi}{4}} \ln(1+\tan r) \, dr \)。

学生的解答到此为止，没有完成后续的定积分计算。标准答案的后续步骤是计算这个定积分，并最终得到结果 \( \frac{\ln 2}{16} \pi^{2} \)。

因此，学生的解答完成了本题的关键步骤（换元和化简），但未完成最终的计算。考虑到本题满分12分，且主要难点在于极坐标变换和后续的积分技巧，学生完成了前半部分的核心工作。根据部分得分的原则，给予学生大部分分数。

扣分点：未完成最终计算，结果不完整。扣除3分。

得分：9分。

题目总分：9分