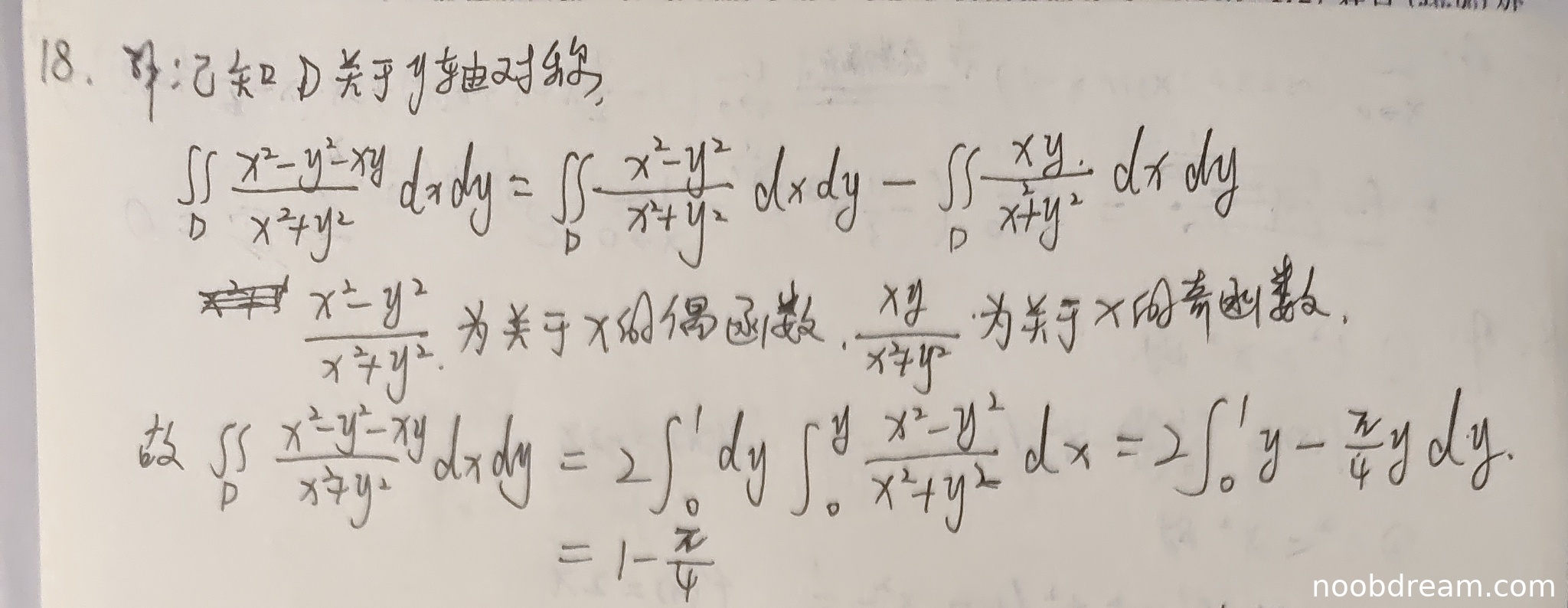
评分及理由

（1）得分及理由（满分10分）

学生作答分为两次识别，但内容实质相同。整体思路与标准答案基本一致：利用区域关于y轴对称，将积分拆分为两部分，其中奇函数部分为零，偶函数部分化为半区域上的二重积分并计算。但在关键的计算步骤中出现了错误：

• 学生计算内层积分 \(\int_{0}^{y} \frac{x^{2}-y^{2}}{x^{2}+y^{2}} dx\) 时，得到结果为 \(y - \frac{\pi}{2} y\)，这相当于 \(y(1 - \frac{\pi}{2})\)。
• 而标准答案中对应部分（即 \(I_1\) 中的 \( -2\iint_{D} \frac{y^2}{x^2+y^2} dxdy \) 在半区域上计算）得到的是 \(\frac{\pi}{4} y\)，因此整个被积函数在半区域上的积分应为 \(y - 2 \cdot \frac{\pi}{4} y = y - \frac{\pi}{2} y\)，这与学生得到的内层积分表达式一致。
• 但是，学生在后续计算 \(2\int_{0}^{1} (y - \frac{\pi}{2} y) dy\) 时，错误地提取了系数，写成了 \(2(1-\frac{\pi}{2})\int_{0}^{1} y dy\)，这实际上是将 \(y - \frac{\pi}{2} y\) 错误地因式分解为 \((1-\frac{\pi}{2})y\)，然后乘以2得到 \(2(1-\frac{\pi}{2})\int_{0}^{1} y dy = 2(1-\frac{\pi}{2}) \cdot \frac{1}{2} = 1 - \frac{\pi}{4}\)。
• 正确的计算应为：\(2\int_{0}^{1} (y - \frac{\pi}{2} y) dy = 2\int_{0}^{1} (1 - \frac{\pi}{2}) y \, dy = 2(1 - \frac{\pi}{2}) \cdot \frac{1}{2} = 1 - \frac{\pi}{2}\)。学生错误地将结果算成了 \(1 - \frac{\pi}{4}\)，这是计算过程中的算术错误。

因此，学生的思路完全正确，但在最后的数值计算上出现了错误。根据评分要求，逻辑错误需要扣分。该错误属于计算错误，导致最终答案不正确。考虑到题目...