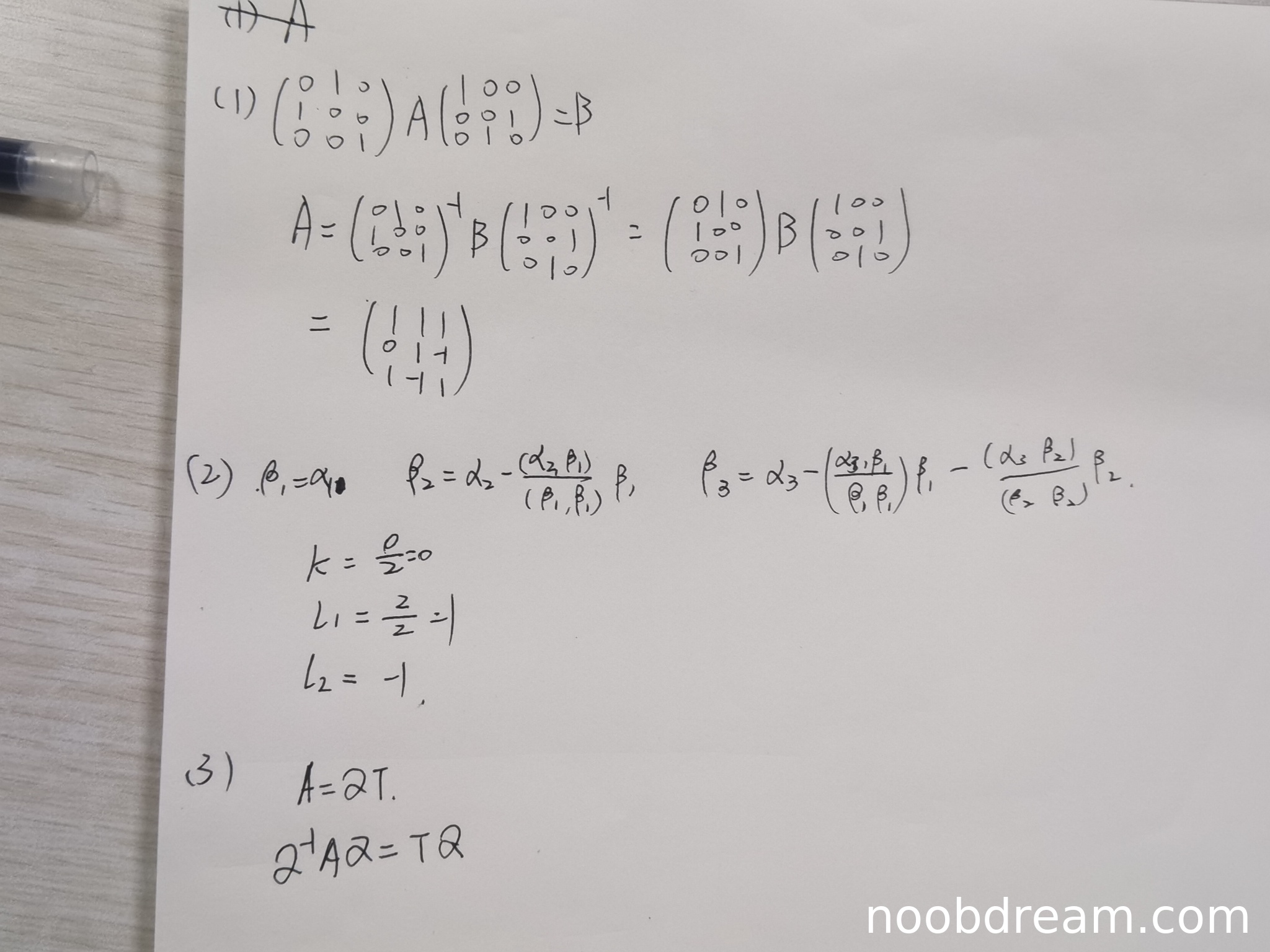
评分及理由

（Ⅰ）得分及理由（满分4分）

学生第一次识别结果中，矩阵运算有误：第二步将列交换矩阵的逆写成了单位矩阵，导致最终结果错误（第三列第二行元素为1，应为-1）。但第二次识别结果完全正确，思路清晰，计算无误。根据“两次识别只要有一次正确则不扣分”的原则，本题不扣分。
得分：4分

（Ⅱ）得分及理由（满分4分）

学生给出了正确的施密特正交化公式。第一次识别中，\(\beta_3\)公式中误写为\(\frac{(\alpha_2,\beta_2)}{(\beta_2,\beta_2)}\)，且给出的\(l_2 = -1\)错误。第二次识别中，公式完全正确，但给出的数值结果\(l_2 = -1\)仍然错误（正确答案应为\(-\frac{1}{3}\)）。计算过程缺失，直接给出错误结果，属于逻辑错误。
扣分：结果错误扣2分。
得分：2分

（Ⅲ）得分及理由（满分4分）

学生仅写出了分解形式\(A=QT\)和一个不相关的等式\(Q^{-1}AQ = TQ\)，完全没有进行正交化、单位化以及求解矩阵\(Q\)和\(T\)的具体过程。答案不完整，未完成题目要求。
扣分：未完成求解，扣4分。
得分：0分

题目总分：4+2+0=6分