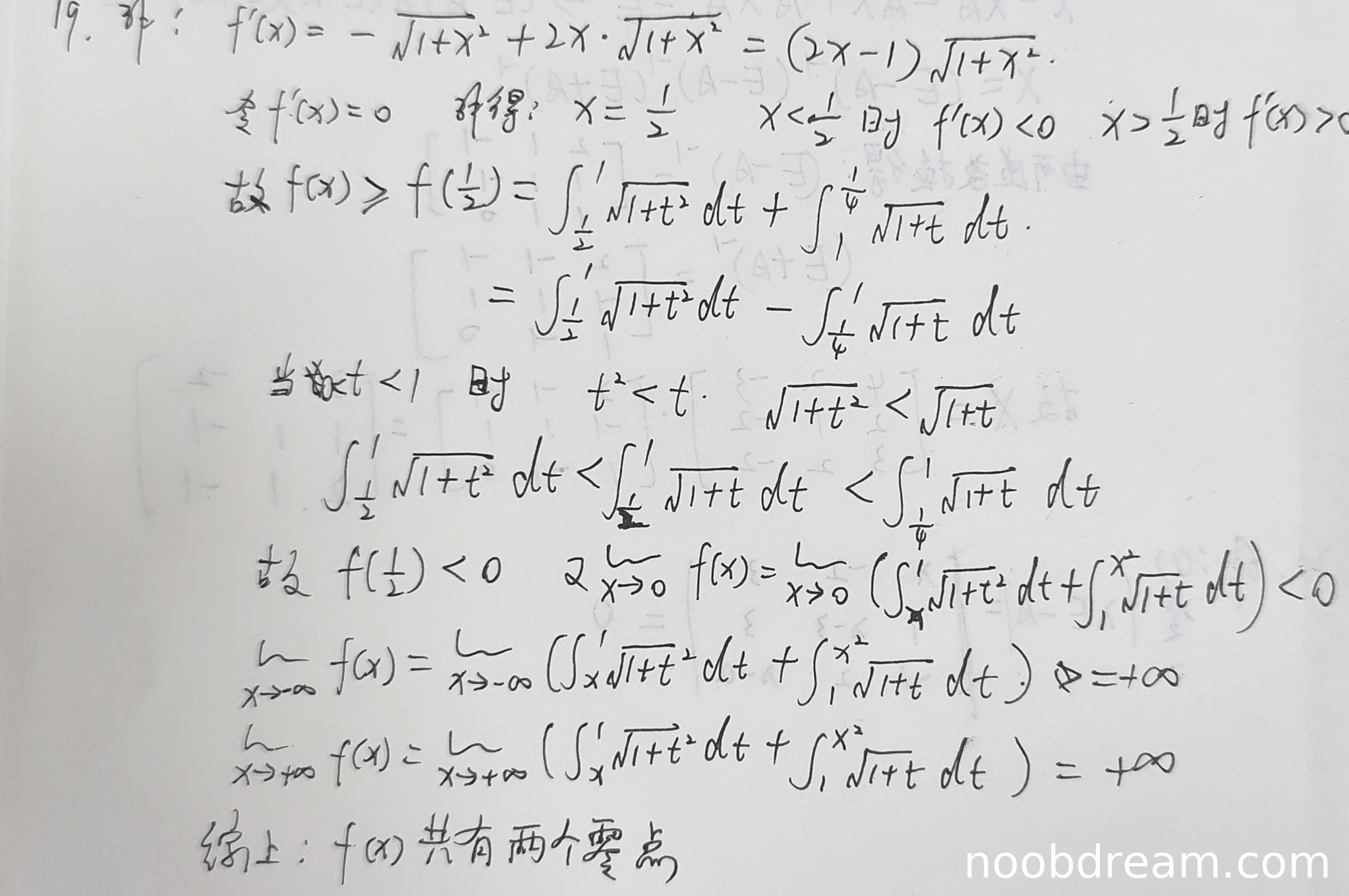
评分及理由

（1）得分及理由（满分10分）

学生作答整体思路与标准答案一致：先求导确定单调性，找到唯一驻点（最小值点），证明最小值小于0，再考察函数在负无穷和正无穷处的极限均为正无穷，从而得出函数在左右两侧各有一个零点，总零点数为2个。主要步骤和结论正确。

但存在以下问题：

1. 在第一次识别结果中，计算 \(f(\frac{1}{2})\) 时写为 \(\int_{1}^{\frac{1}{4}}\sqrt{1+t}dt\)，但在后续比较积分时，错误地写成了 \(\int_{\frac{1}{2}}^{1}\sqrt{1+t^{2}}dt<\int_{\frac{1}{2}}^{1}\sqrt{1+t}dt<\int_{\frac{1}{4}}^{1}\sqrt{1+t}dt\)，并由此得出 \(f(\frac{1}{2})<0\)。虽然结论正确，但中间的比较逻辑不够严谨（标准答案通过拆分积分区间并比较被积函数来严格证明）。不过，学生抓住了核心：在 \(t \in (\frac{1}{2}, 1)\) 时 \(\sqrt{1+t^2} < \sqrt{1+t}\)，且 \(\int_{\frac{1}{4}}^{\frac{1}{2}} \sqrt{1+t} dt > 0\)，因此 \(f(\frac{1}{2}) < 0\) 的结论是合理的。此处逻辑表述有瑕疵，但不影响最终结论，扣1分。
2. 在第一次识别结果中，出现了 \(\lim\limits_{x\rightarrow0}f(x)<0\) 的步骤，这个极限计算并非必要，且学生没有给出具体值，只是断言小于0。虽然 \(f(0)\) 确实小于0（可通过计算验证），但此处直接写极限符号不妥（应写 \(f(0)\)）。不过，这个步骤对零点个数的判断没有实质性影响，且可能为识别错误（将 \(x \to -\infty\) 误识别为 \(x \to 0\)？）。根据禁止扣分原则，若判断为误写则不扣分。结合上下文，学生重点考察了 \(x \to \pm\infty\) 的极限，因此此处的 \(x \to 0\) 可能为笔误或识别错误，不扣分。
3. 在第二次识别结果中，计算 \(f(\frac{1}{2})\) 时写成了 \(\int_{1}^{\frac{1}{x}}\sqrt{1+t}dt\)，这显然是识别错误（应为 \(\frac{1}{4}\)）。根据禁止扣分原则，字符识别错误不扣分。
4. 学生没有像标准答案那样严格计算 \(\lim_{x\to +\infty} f(x)\) 的极限（通过比较增长率），而是直接写出结果为 \(+\infty\)。虽然结论正确，但缺少关键步骤（需说明当 \(x \to +\infty\) 时，第二项的增长速度远大于第一项）。此处逻辑不够完整，扣1分。

综上，学生答案核心思路正确，结论正确，但在严格性和完整性上有两处不足，共扣2分。

得分：8分（满分10分）。

题目总分：8分