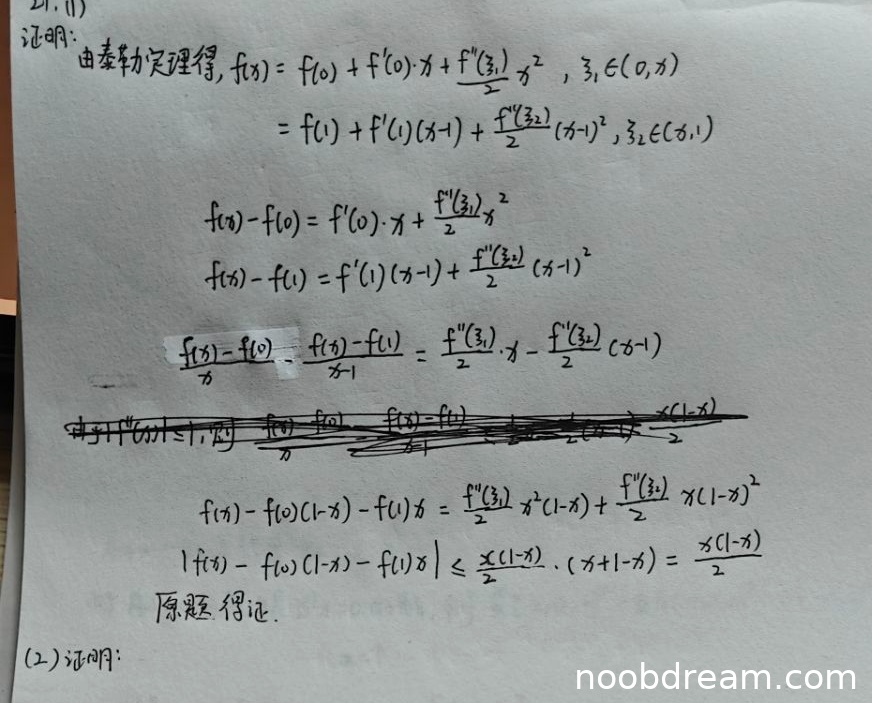
评分及理由

（1）得分及理由（满分6分）

学生尝试使用泰勒公式进行证明，思路与标准答案不同但方向正确。然而，在推导过程中存在多处逻辑错误和跳跃：

1. 从两个泰勒展开式出发，得到 \(f(x)-f(0)=f'(0)x+\frac{f''(\xi_1)}{2}x^2\) 和 \(f(x)-f(1)=f'(1)(x-1)+\frac{f''(\xi_2)}{2}(x-1)^2\) 是正确的。
2. 但后续构造 \(\frac{f(x)-f(0)}{x}-\frac{f(x)-f(1)}{x-1}\) 并声称它等于 \(\frac{f''(\xi_1)}{2}x-\frac{f''(\xi_2)}{2}(x-1)\) 是错误的。实际上，由两个泰勒式分别除以 \(x\) 和 \(x-1\) 后相减，会得到： \[ \frac{f(x)-f(0)}{x} = f'(0)+\frac{f''(\xi_1)}{2}x,\quad \frac{f(x)-f(1)}{x-1}=f'(1)+\frac{f''(\xi_2)}{2}(x-1) \] 相减后应为： \[ \frac{f(x)-f(0)}{x}-\frac{f(x)-f(1)}{x-1}=[f'(0)-f'(1)]+\frac{f''(\xi_1)}{2}x-\frac{f''(\xi_2)}{2}(x-1) \] 学生忽略了 \(f'(0)-f'(1)\) 项（已知 \(f'(0)=f'(1)\)，所以该项为0，但推导中未说明直接舍去，逻辑不完整）。
3. 接着，学生直接写出 \(f(x)-f(0)(1-x)-f(1)x=\frac{f''(\xi_1)}{2}x^2(1-x)+\frac{f''(\xi_2)}{2}x(1-x)^2\)，这一步缺乏推导过程，是凭空出现的，与前面的式子没有直接代数关系，属于逻辑断裂。
4. 最后利用 \(|f''|\le 1\) 得到不等式，虽然形式正确，但中间推导不严谨，关键等式未建立。

由于证明的核心步骤存在严重逻辑错误，不能给满分。考虑到学生知道使用泰勒公式并试图利用二阶导有界，有一定思路，但执行错误较多，扣分较多。给分：2分。

（2）得分及理由（满分6分）

学生只写了“(2)证明：”后无内容，没有给出第二部分证明。因此本题未作答，得0分。

题目总分：2+0=2分