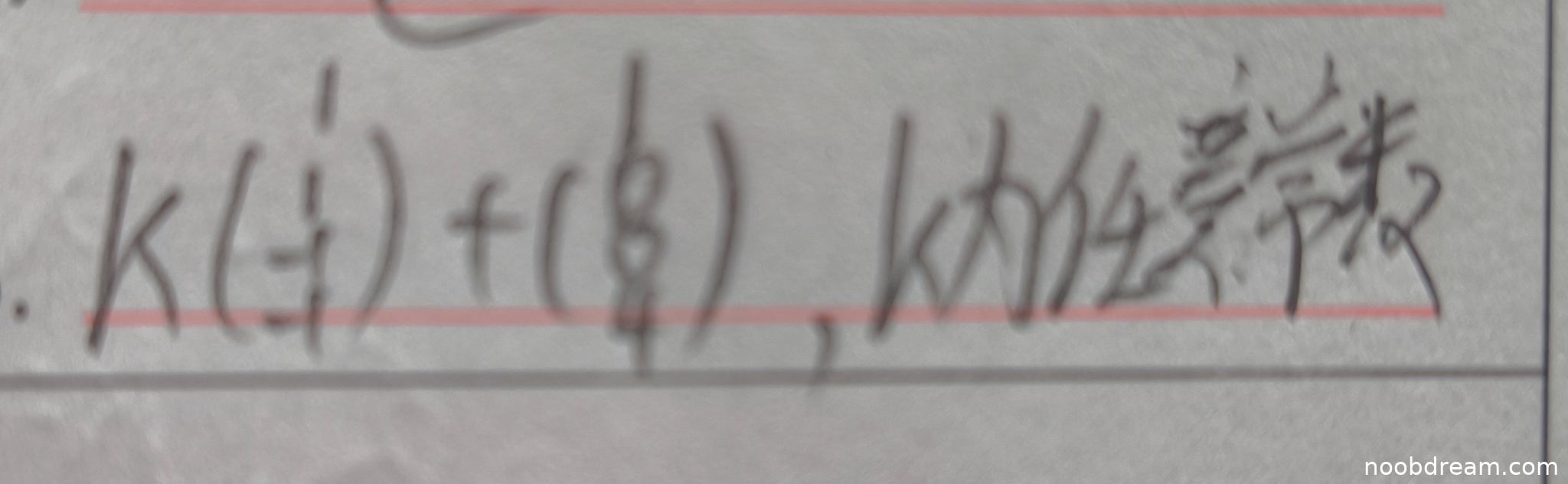
评分及理由

（1）得分及理由（满分5分）

学生答案：第1次识别结果为“k(÷)+(8)”，第2次识别结果为“$k(-\frac{1}{4})+(\frac{1}{8})$”。

标准答案：$k\begin{pmatrix}1\\1\\ - 1\\ - 1\end{pmatrix}+\begin{pmatrix}1\\0\\0\\4\end{pmatrix}$，$k$为任意常数。

分析：

1. 学生两次识别的结果均与标准答案在形式和数值上完全不同。第1次识别结果“k(÷)+(8)”无法构成一个有效的向量表达式，无法对应到通解的结构“k * 特解向量 + 特解向量”。
2. 第2次识别结果“$k(-\frac{1}{4})+(\frac{1}{8})$”是一个标量表达式，而方程 $Ax = a_1 + 4a_4$ 的解 $x$ 是一个4维向量，因为矩阵 $A$ 有4列。学生的答案维度错误，且具体数值与标准答案的特解 $(1,0,0,4)^T$ 和齐次基础解系 $(1,1,-1,-1)^T$ 没有任何关联。
3. 根据题目条件 $a_1, a_2, a_3$ 线性无关且 $a_1 + a_2 = a_3 + a_4$，可以推导出 $a_4 = a_1 + a_2 - a_3$。代入方程 $Ax = a_1 + 4a_4 = a_1 + 4(a_1 + a_2 - a_3) = 5a_1 + 4a_2 - 4a_3$。设 $x = (x_1, x_2, x_3, x_4)^T$，则 $Ax = x_1a_1 + x_2a_2 + x_3a_3 + x_4a_4 = x_1a_1 + x_2a_2 + x_3a_3 + x_4(a_1 + a_2 - a_3) = (x_1+x_4)a_1 + (x_2+x_4)a_2 + (x_3-x_4)a_3$。由于 $a_1, a_2, a_3$ 线性无关，比较系数可得方程组： $\begin{cases} x_1 + x_4 = 5 \\ x_2 + x_4 = 4 \\ x_3 - x_4 = -4 \end{cases}$ 解得通解为 $x = \begin{pmatrix}5 - x_4 \\ 4 - x_4 \\ -4 + x_4 \\ x_4 \end{pmatrix} = x_4 \begin{p...