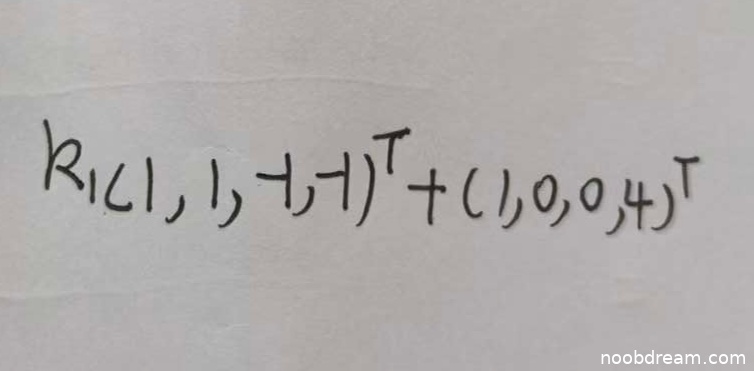
评分及理由

（1）得分及理由（满分5分）

学生作答的两次识别结果分别为：
1. $R_{1}(1,1,-1,-1)^{T}+(1,0,0,4)^{T}$
2. $k_{1}(1,1, - 1,-1)^{\text{T}}+(1,0,0,4)^{\text{T}}$

标准答案为：$k\begin{pmatrix}1\\1\\ - 1\\ - 1\end{pmatrix}+\begin{pmatrix}1\\0\\0\\4\end{pmatrix}$，$k$为任意常数。

评分分析：
1. 结构判断： 学生答案的结构是“齐次通解 + 特解”的形式，这与标准答案的结构完全一致。
2. 特解判断： 学生的特解为 $(1,0,0,4)^T$，与标准答案的特解 $(1,0,0,4)^T$ 完全相同。
3. 基础解系判断： 学生给出的齐次通解部分为 $(1,1,-1,-1)^T$ 的倍数，与标准答案的基础解系 $(1,1,-1,-1)^T$ 完全相同。
4. 参数符号： 学生第一次识别使用了 $R_1$，第二次识别使用了 $k_1$，标准答案使用 $k$。参数符号的差异（如 $R_1$, $k_1$, $k$）不影响答案的正确性，均表示任意常数。
5. 书写格式： 学生答案使用了转置符号 $^T$ 或 $\text{T}$，标准答案使用了列向量形式，二者在数学上等价，不影响正确性。

结论： 学生的答案在数学本质上与标准答案完全一致，因此本题得满分。

得分：5分。

题目总分：5分