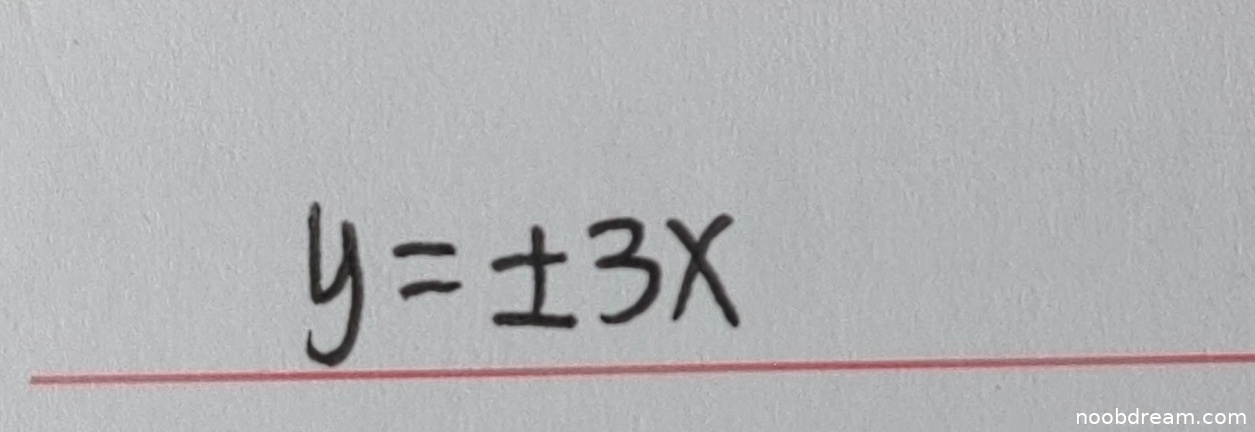
评分及理由

（1）得分及理由（满分5分）

学生两次识别结果均为“y = ±3x”。标准答案为“y = ± 3”。

分析：函数 \(f(x)=\frac{1}{2} \ln \frac{3+x}{3-x}\) 的定义域为 \((-3, 3)\)，值域为 \((-\infty, +\infty)\)。其反函数 \(g(x)\) 的定义域为 \((-\infty, +\infty)\)，值域为 \((-3, 3)\)。因此，曲线 \(y = g(x)\) 有两条水平渐近线：当 \(x \to +\infty\) 时，\(g(x) \to 3^-\)；当 \(x \to -\infty\) 时，\(g(x) \to -3^+\)。所以渐近线方程为 \(y = 3\) 和 \(y = -3\)，即 \(y = \pm 3\)。

学生答案“y = ±3x”表示两条过原点的斜线 \(y=3x\) 和 \(y=-3x\)，这与反函数的值域有界（介于-3和3之间）的性质矛盾，因此答案错误。该错误属于核心逻辑错误，并非字符误写（如将“3”误写为“3x”），因此需要扣分。

根据评分规则，本题为填空题，正确得5分，错误得0分。学生答案错误，故得0分。

题目总分：0分