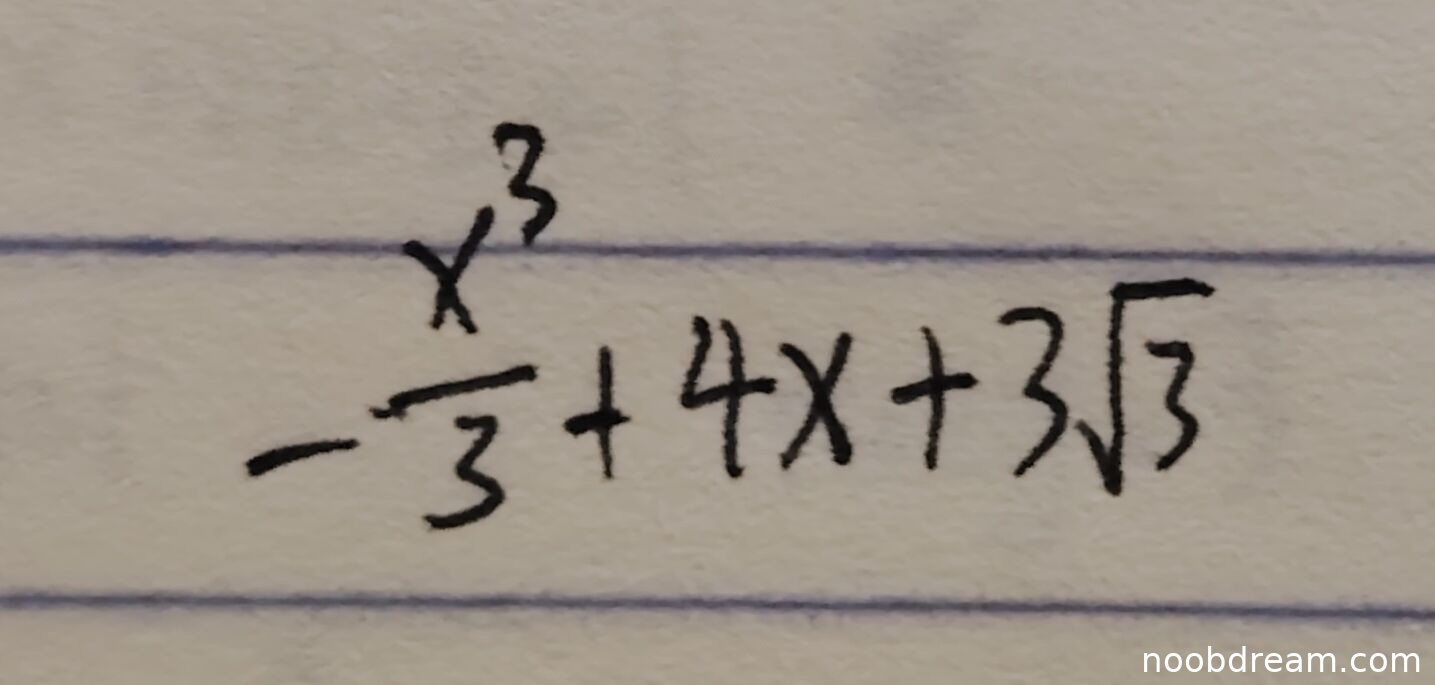
评分及理由

（1）得分及理由（满分5分）

学生给出的两个识别结果均为 \(-\frac{x^{3}}{3}+4x + 3\sqrt{3}\)，这与标准答案 \(\sqrt{3}+\frac{4}{3} \pi\) 完全不同。

题目要求计算曲线 \(y=\int_{-\sqrt{3}}^{x} \sqrt{3-t^{2}} ~d t\) 的弧长。这是一个定积分定义的函数，其弧长公式为 \(L = \int_{a}^{b} \sqrt{1 + [y'(x)]^2} dx\)。首先需要求导 \(y'(x) = \sqrt{3 - x^2}\)，然后代入弧长公式。被积函数 \(\sqrt{1 + (3 - x^2)} = \sqrt{4 - x^2}\)。接下来需要确定积分区间。原函数 \(y(x)\) 的定义域由被积函数 \(\sqrt{3-t^2}\) 决定，即 \(t \in [-\sqrt{3}, \sqrt{3}]\)，所以 \(x\) 的取值区间也是 \([-\sqrt{3}, \sqrt{3}]\)。因此弧长 \(L = \int_{-\sqrt{3}}^{\sqrt{3}} \sqrt{4 - x^2} dx\)。这个积分可以通过几何意义（半圆面积）或三角代换来计算，结果为 \(\sqrt{3} + \frac{4\pi}{3}\)。

学生给出的答案是一个关于 \(x\) 的多项式加上常数，这完全不符合弧长应为一个常数的基本事实。这表明学生可能错误地理解了题目，例如可能计算了原函数 \(y(x)\) 本身，或者进行了错误的运算。这是一个根本性的逻辑错误，答案与标准答案不符。

根据评分要求，本题为填空题，正确则给5分，错误则给0分，禁止给步骤分。因此，本题得分为0分。

题目总分：0分