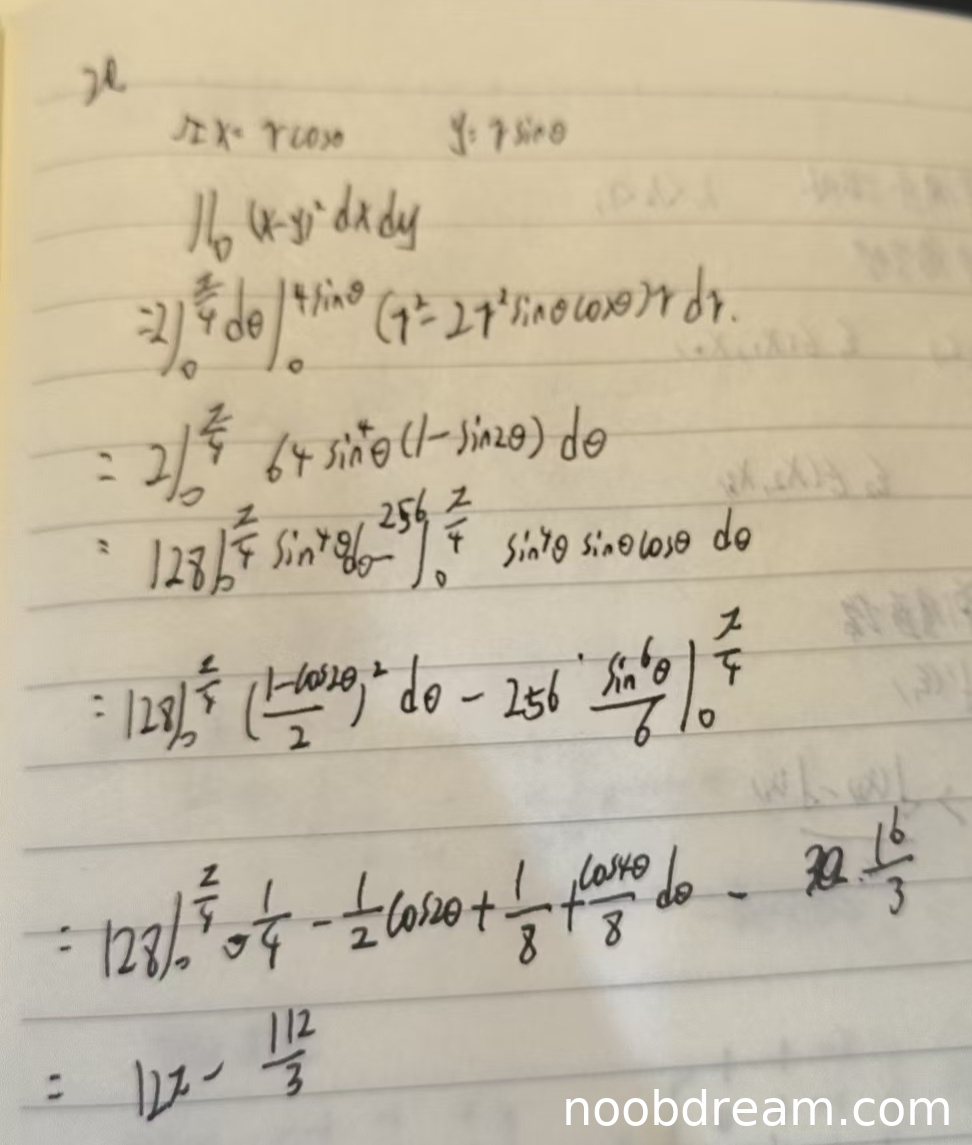
评分及理由

（1）得分及理由（满分12分）

学生作答给出了两次识别结果，核心思路是利用极坐标变换计算二重积分。第一次识别结果的计算过程存在多处错误，例如积分上限误写为 \(4\sin\theta\)（应为 \(4\cos\theta\) 或根据对称性调整）、三角函数展开和积分计算错误，最终得到错误答案 \(12\pi - \frac{112}{3}\)。第二次识别结果详细阐述了极坐标变换过程，但同样基于错误的积分区域（推测区域与题目不符，实际上限应为 \(4\cos\theta\) 或 \(4\sin\theta\) 取决于对称部分的选取），并在计算 \(\int \sin^4\theta d\theta\) 时得到 \(\frac{3\pi}{32} - \frac{1}{4}\)，该结果错误（正确值应为 \(\frac{3\pi}{32} - \frac{1}{4} + \frac{1}{32}\sin\pi = \frac{3\pi}{32} - \frac{1}{4}\)，但代入后续计算时系数处理有误，且最终答案与标准答案 \(12\pi - \frac{16}{3}\) 不一致）。

尽管学生思路正确（利用对称性和极坐标），但关键步骤——积分区域的极坐标表示出现错误（\(r\) 的上限应为 \(4\cos\theta\) 而非 \(4\sin\theta\)，若按 \(D_1\) 的定义），导致后续计算全部错误。根据评分要求，逻辑错误需扣分。由于该题为计算题，最终答案错误，且核心步骤（积分限）错误，应扣除大部分分数。考虑到学生展示了正确的解题框架（对称性、极坐标变换、展开被积函数），给予部分步骤分。

得分：4分（满分12分）。扣分理由：积分区域极坐标表示错误（-4分），三角函数积分计算错误（-2分），最终答案错误（-2分）。

题目总分：4分