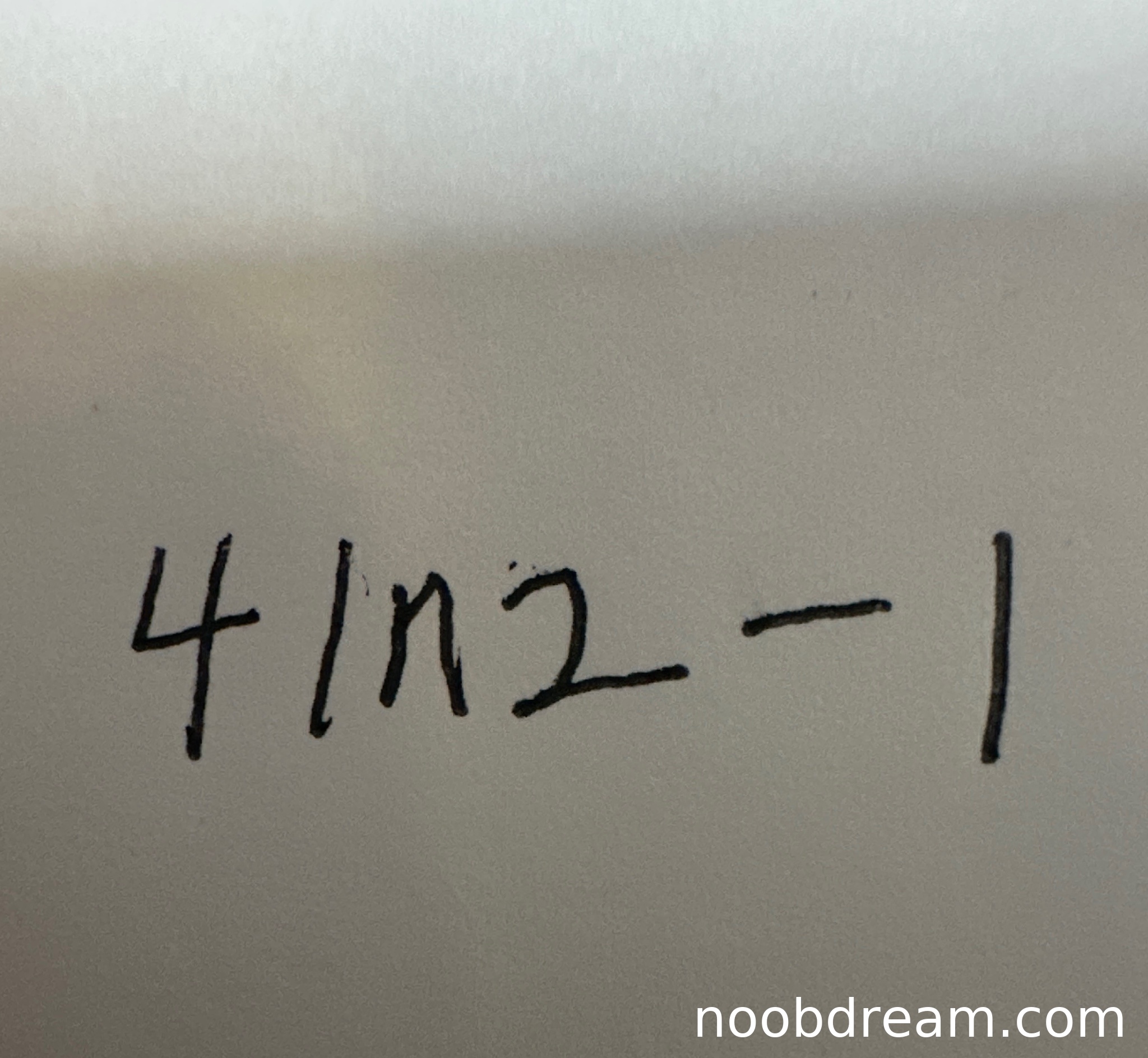
评分及理由

（1）得分及理由（满分5分）

本题要求计算函数 \( f(x) = \ln(2+x) \) 在区间 \([0, 2]\) 上的平均值。函数在区间上的平均值公式为： \[ \frac{1}{b-a} \int_a^b f(x) \, dx \] 代入 \( a=0, b=2, f(x)=\ln(2+x) \)，得到： \[ \text{平均值} = \frac{1}{2-0} \int_0^2 \ln(2+x) \, dx = \frac{1}{2} \int_0^2 \ln(2+x) \, dx \] 计算积分：令 \( u = 2+x \)，则 \( du = dx \)，当 \( x=0 \) 时 \( u=2 \)，当 \( x=2 \) 时 \( u=4 \)。 \[ \int_0^2 \ln(2+x) \, dx = \int_2^4 \ln u \, du = \left[ u \ln u - u \right]_2^4 \] 代入计算： \[ (4 \ln 4 - 4) - (2 \ln 2 - 2) = (4 \cdot 2\ln 2 - 4) - (2\ln 2 - 2) = (8\ln 2 - 4) - (2\ln 2 - 2) = 6\ln 2 - 2 \] 因此，平均值为： \[ \frac{1}{2} (6\ln 2 - 2) = 3\ln 2 - 1 \] 标准答案为 \( 3\ln 2 - 1 \)。学生两次识别结果均为 \( 4\ln 2 - 1 \)，与标准答案不符。虽然可能存在字符识别问题（例如将“3”识别为“4”），但根据规则，对于识别结果，若两次均错误，则判定为答案错误。因此，本题得分为0分。

题目总分：0分