评分及理由

（1）得分及理由（满分6分）

学生作答中，第一次识别结果给出了对矩阵A进行初等行变换的过程，并得出秩为2，且指出α₁,α₂线性无关，从而证明它们是极大线性无关组。思路正确，但变换结果与标准答案不完全一致（标准答案化为行最简形是 \(\begin{pmatrix} 1 & 0 & -1 & 1 \\ 0 & 1 & 1 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}\)，学生第一次识别结果为 \(\begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}\)，这仍是阶梯形，秩为2的判断正确）。不过学生在证明开头写“设 \(a_3 = a_2 - a_1\)”等表达式有误（向量写错），但后续矩阵写的是正确的，可能是识别误差。整体逻辑正确，结论正确。第二次识别结果中向量计算明显有误（如α₃计算错误），但根据“只要其中有一次回答正确则不扣分”的原则，以第一次识别为准。因此（1）部分给满分6分。

（2）得分及理由（满分6分）

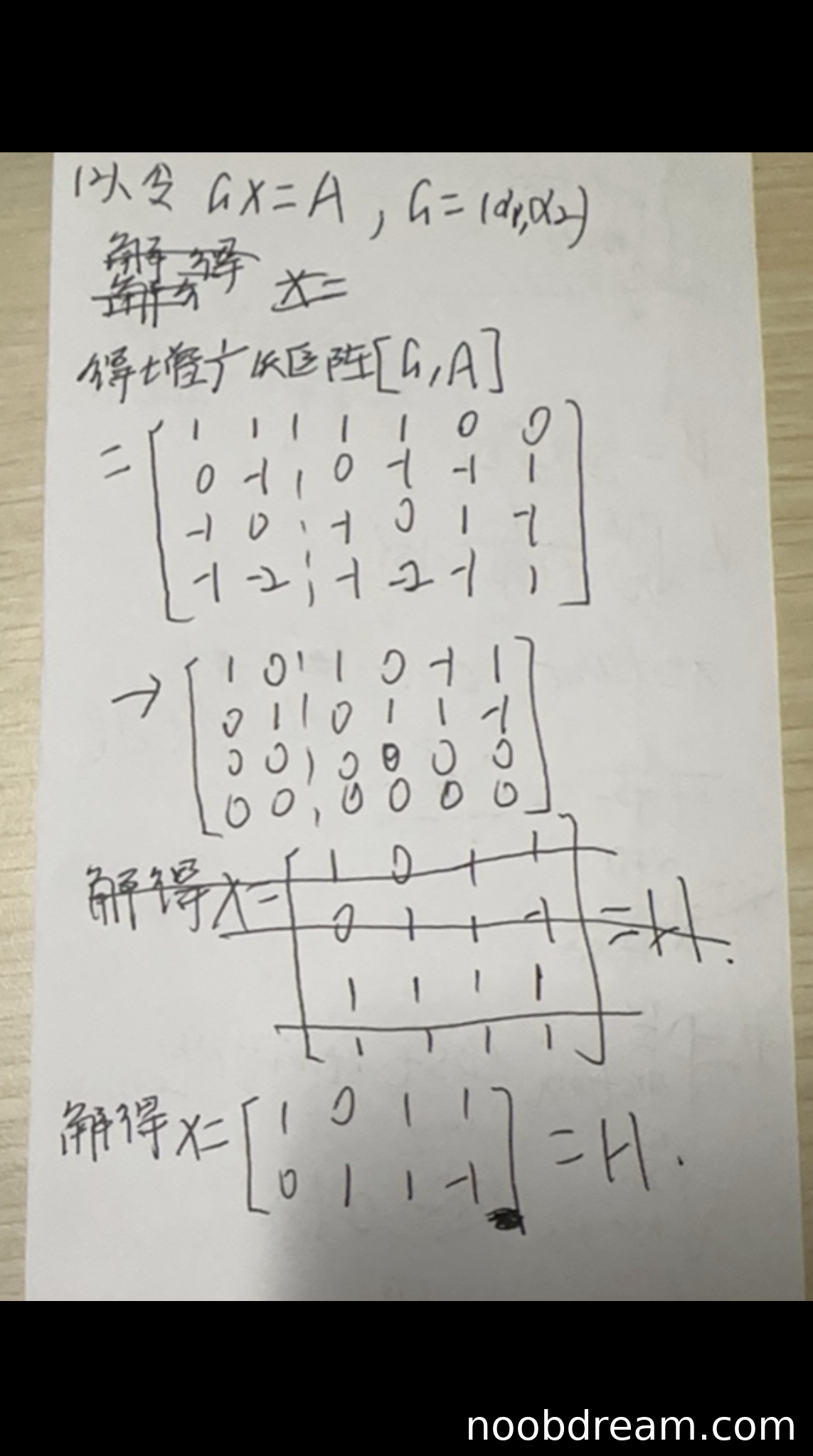
学生设 \(GX = A\)，通过增广矩阵 \([G, A]\) 行变换求解 \(X\)（即 \(H\)）。第一次识别结果中，增广矩阵书写有误（列数不对，应为4列，但写了6列），但行变换后得到 \(X = \begin{pmatrix} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & -1 \end{pmatrix}\)，这与标准答案 \(H = \begin{pmatrix} 1 & 0 & -1 & 1 \\ 0 & 1 & 1 & -1 \end{pmatrix}\) 相比，第3列不同（学生是1,1，标准是-1,1）。这可能是计算错误或识别错误。由于题目要求求 \(A^{10}\)，若H错误会导致后续计算错误，但学生答案中未给出 \(A^{10}\) 的计算，因此（2）部分只评价求H的过程。H的结果有误，但思路正确（用线性表示求系数矩阵），且部分正确（第1,2,4列正确）。根据部分正确的情况，给予部分分数，扣2分。得4分。

题目总分：6+4=10分