写在前面（因为后面不好加）

这个答案非我原创，是我穷途末路的时候，看到一个写得很和我胃口的答案，研究了一两天写出来的个人理解，我个人也是菜狗子，如有不足，欢迎指正。

正文

这是一个很容易看出来要用贪心（bushi）但是很难想具体的贪心策略的题目（主要是我经验不足，没有看懂解题方法）。

为什么容易看出来贪心呢？因为这道题拥有着贪心经典的输入格式：

第一行先输入一堆限制条件，包括最大油量、总行驶路程，每单位油能走的距离，等同于买饮料的钱。

然后给了加油站（饮料）的个数N。

剩下的 N 行分别输入汽油单价和加油站的距离，等同于饮料的容量和价钱。

真的，这两个题目的输入简直长得一模一样的。

接下来按照贪心算法解题的通用步骤来理解这道题：

以第一组输入为例，我们可以画一张图来理解这个问题：

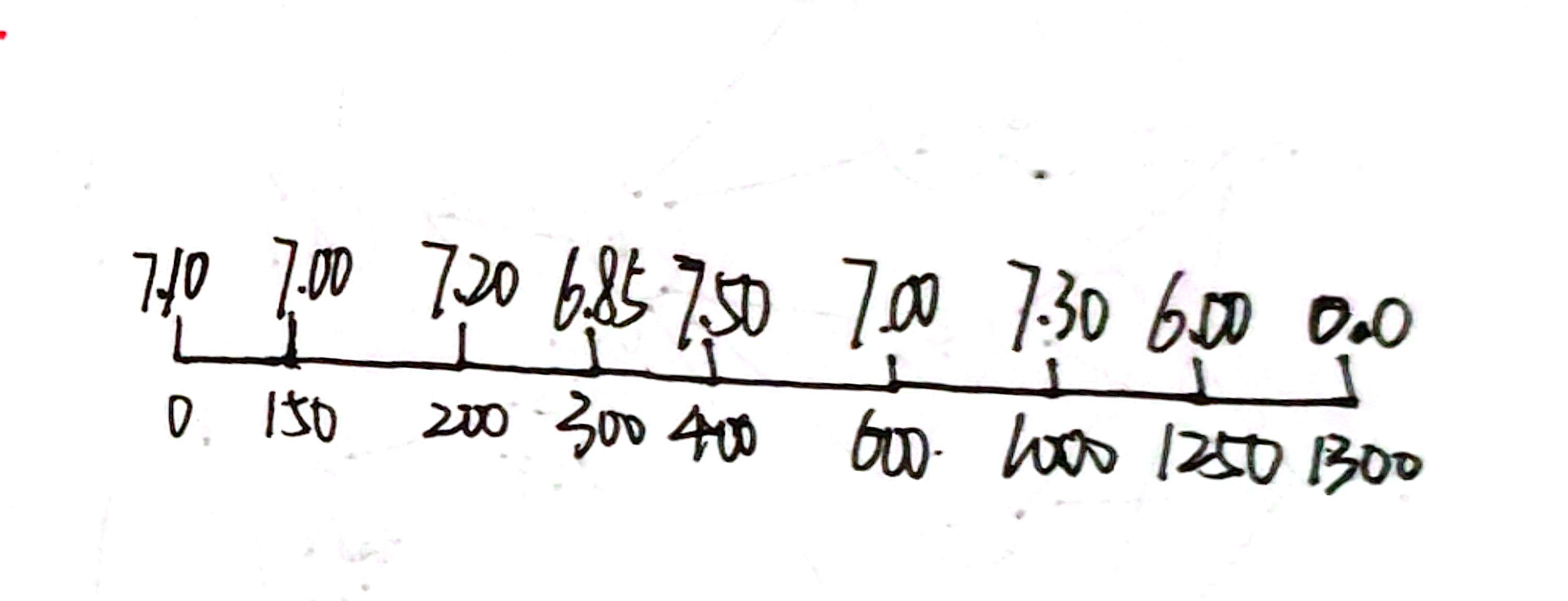
如上图，下侧是加油站距杭州城的距离，上侧是加油站的汽油单价。

车子的任务就是在成功到达终点站的同时尽量用便宜的油，因为一定要走1300的路，单位距离使用的油价越小越好。

要在行驶的路上尽可能使用便宜的油，我们就要往低价油的加油站跑，而且要尽快从高价油切换成低价油（找加油站部分），而且加油的时候尽可能少装高价油（加油部分）。因为每装着高价油多跑一个单位距离，平均的油价就会更高一点。

接下来我们从以上加粗的三个子问题入手得到局部最优解。

如果有的话，我们需要在最大的行驶距离内找到最近的比当前便宜的加油站。如果只有比当前贵的加油站，我们需要在最大的行驶距离内找到最便宜的加油站，无论距离如何。

为什么找「最近的便宜加油站」，而非「最大范围内更便宜的加油站」？因为「更远的更便宜站」需要先消耗当前的高价油开到那里，反而会增加总成本；而「最近的便宜站」能让你「尽早切换到低价油」，是局部最优的选择。

为什么不能找「最近的加油站」（哪怕贵一点）？ 总费用 = 油价 × 油量，油价的涨幅通常远大于 “短途少耗的油量” 带来的节省，选最近的贵站会导致后续不得不加...