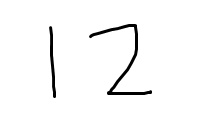
评分及理由

（1）得分及理由（满分5分）

学生两次识别的答案均为“12”。标准答案为“4”。学生的答案与标准答案不符。

曲率半径的计算需要先求出曲线在给定点的曲率。对于隐函数给出的曲线，通常需要计算一阶和二阶导数。在点(0,1)处，代入方程验证该点在曲线上。通过隐函数求导或参数化方法可以求得该点处的一阶导数和二阶导数，进而利用曲率公式 \( k = \frac{|y''|}{(1+y'^2)^{3/2}} \) 计算曲率，曲率半径 \( R = 1/k \)。正确的计算过程得到 \( R = 4 \)。学生答案“12”是一个错误的计算结果，表明其计算过程中存在逻辑或计算错误。

根据评分规则，答案错误得0分。

题目总分：0分