评分及理由

（1）得分及理由（满分3分）

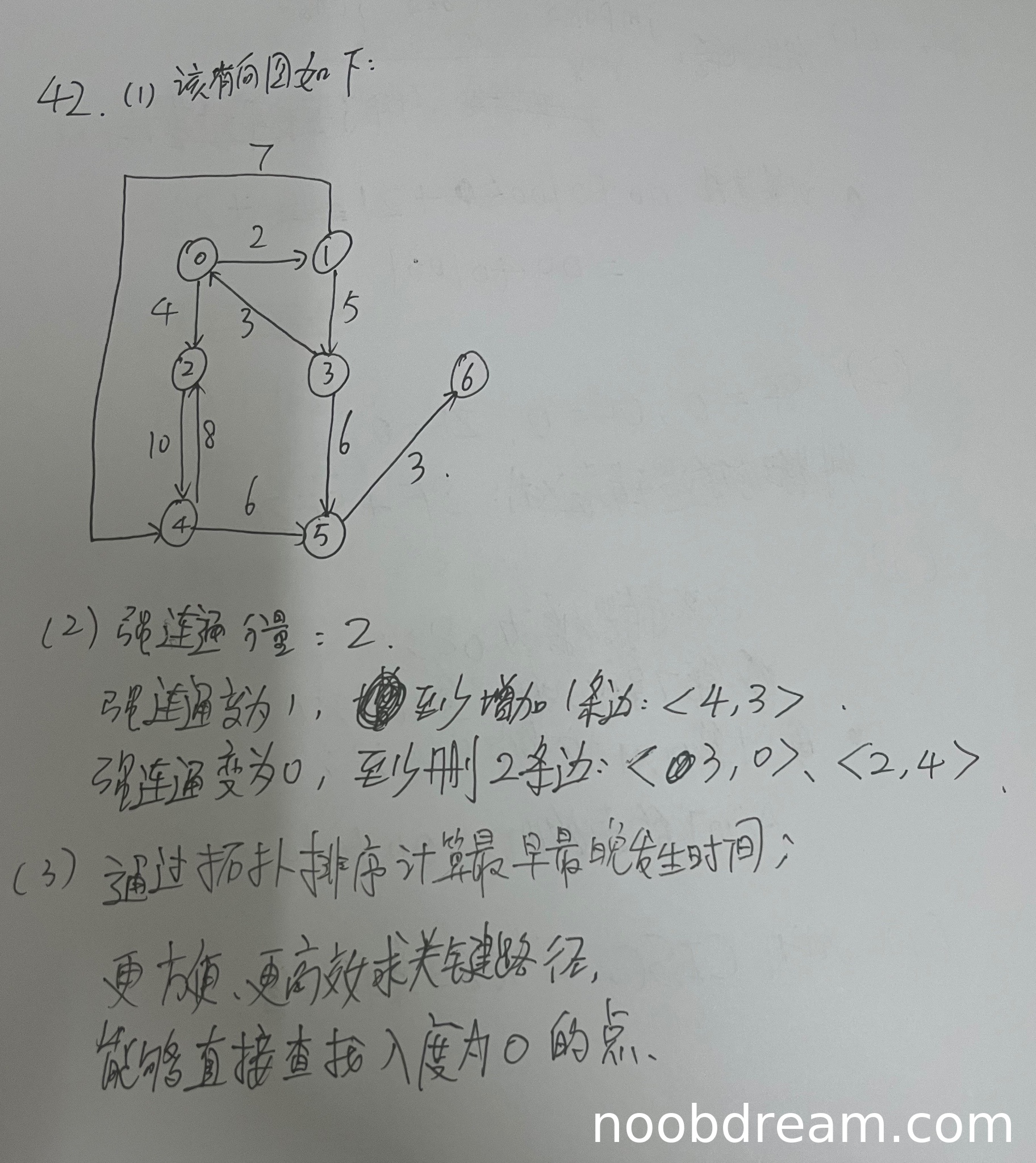
学生作答中给出了图的边信息，但存在错误：标准图中没有0→3（权3）的边，且多出了2→3（权8）的边（实际应为C↔E的双向边，即2→4权10和4→2权8）。此外，学生未画出完整图形，仅描述了边。根据标准答案要求，需正确画出所有边和顶点。识别结果中边描述有误，且未提供图示，因此扣2分。得1分（仅部分正确）。

（2）得分及理由（满分3分）

学生回答强连通分量数量为2（错误，应为4），扣1分；添加边方案为<4,3>（即E→D），但标准答案要求添加边使强连通分量数量变为1，此方案可能有效（例如G→D或E→D等），但未指定具体顶点名称（用编号表示），且未说明效果，可视为部分正确，扣0.5分；删除边方案为<3,0>（D→A）和<2,4>（C→E），这两条边删除后确实可破坏强连通分量（{A,B,D}和{C,E}），使数量大于1的强连通分量变为0，方案正确，得1分。本小题总得分：1.5分（强连通分量数量错误扣1分，添加边部分正确扣0.5分，删除边正确得1分）。

（3）得分及理由（满分3分）

学生回答“通过拓扑排序计算最早最晚发生时间”正确，但未说明判断关键路径存在的前提（检测环和验证AOE网条件），扣1分；“更方便、更高效求关键路径”过于笼统，未指出十字链表直接访问入边的优势（标准答案要求对比邻接表），扣1分；“能够直接查找入度为0的点”不准确（十字链表优势在入边访问而非查找入度），扣1分。得0分。

题目总分：1+1.5+0=2.5分