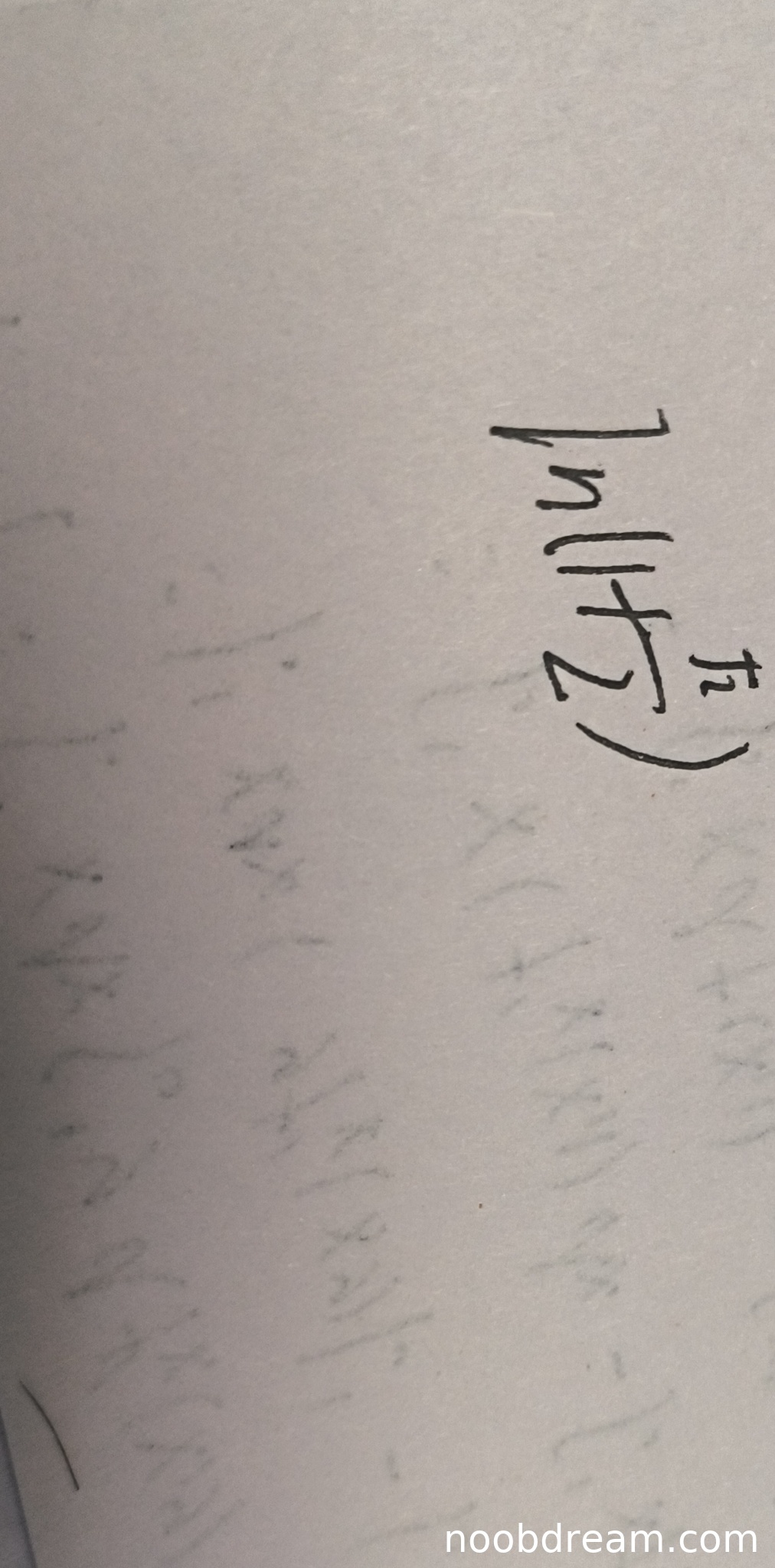
评分及理由

（1）得分及理由（满分4分）

本题考察曲线弧长的计算。曲线方程为 \(y = \int_0^x \tan t \, dt\)，弧长公式为 \(s = \int_0^{\pi/4} \sqrt{1 + (y')^2} \, dx\)。由于 \(y' = \tan x\)，代入得 \(s = \int_0^{\pi/4} \sqrt{1 + \tan^2 x} \, dx = \int_0^{\pi/4} \sec x \, dx\)。计算该积分得 \(s = \ln|\sec x + \tan x| \Big|_0^{\pi/4} = \ln(\sqrt{2} + 1)\)。

学生第一次识别结果为 \(\ln(1+\frac{z}{2})\)，其中"z"可能是识别错误（应为数字"2"），但即使修正为 \(\ln(1+\frac{2}{2}) = \ln 2\)，仍与标准答案 \(\ln(\sqrt{2}+1)\) 不符。第二次识别结果为 \(\ln(1 + x)\)，其中"x"可能是识别错误（应为根号形式），但表达式形式与标准答案差异较大。两次识别结果均未得到正确答案，且存在明显的逻辑错误（未能正确计算积分或简化表达式）。

根据评分规则，答案错误得0分。

题目总分：0分